题目内容
若曲线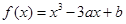 在点
在点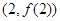 处与直线
处与直线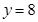 相切,则
相切,则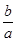 为 .
为 .
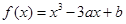 在点
在点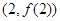 处与直线
处与直线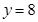 相切,则
相切,则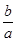 为 .
为 .6
试题分析:由题意可知,曲线
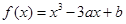 的导数为
的导数为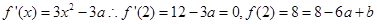
那么联立方程组可知a=4,b=24,因此可知
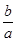 的值为6,故答案为6.
的值为6,故答案为6.点评:解决该试题的关键是利用导数的几何意义表示的切线的斜率得到参数a,b的关系式,进而求解得到表达式的值,属于基础题。

练习册系列答案
相关题目
题目内容
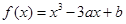 在点
在点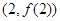 处与直线
处与直线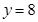 相切,则
相切,则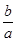 为 .
为 .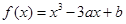 的导数为
的导数为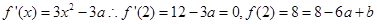
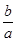 的值为6,故答案为6.
的值为6,故答案为6.