题目内容
(本小题满分12分)
设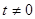 ,点P(
,点P(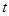 ,0)是函数
,0)是函数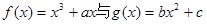 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(1)用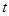 表示a,b,c;
表示a,b,c;
(2)若函数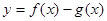 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求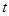 的取值范围.
的取值范围.
设
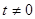 ,点P(
,点P(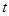 ,0)是函数
,0)是函数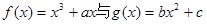 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.(1)用
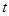 表示a,b,c;
表示a,b,c;(2)若函数
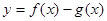 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求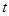 的取值范围.
的取值范围.(1)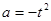 ,
,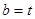 ,
,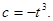 (2)
(2)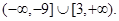
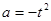 ,
,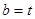 ,
,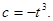 (2)
(2)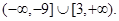
试题分析:(I)因为函数
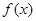 ,
,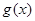 的图象都过点(
的图象都过点(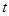 ,0),所以
,0),所以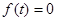 ,
,即
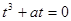 .因为
.因为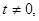 所以
所以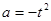 .
. 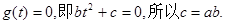 ---2分
---2分又因为
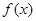 ,
,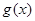 在点(
在点(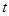 ,0)处有相同的切线,所以
,0)处有相同的切线,所以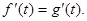
而
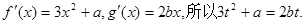 --------4分
--------4分将
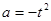 代入上式得
代入上式得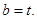 因此
因此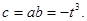 故
故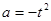 ,
,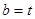 ,
,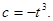 ---6分
---6分(II)
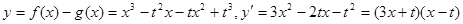 .---7分
.---7分当
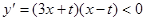 时,函数
时,函数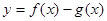 单调递减.
单调递减.由
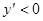 ,若
,若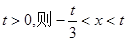 ;若
;若 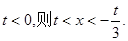 -------9分
-------9分 由题意,函数
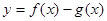 在(-1,3)上单调递减,则
在(-1,3)上单调递减,则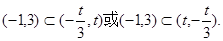 所以
所以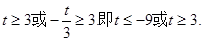 ---11分
---11分所以
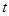 的取值范围为
的取值范围为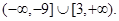 ----12分
----12分点评:利用导数求函数的单调区间,实质上就是求导数>0或导数<0的解集,这样问题就转化为了解不等式,尤其是解含参不等式更为常见。此题是导数中的典型题型,我们要熟练掌握。

练习册系列答案
相关题目
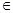 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;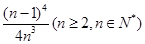 ∈N*).
∈N*).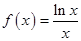 的单调递增区间是 .
的单调递增区间是 . 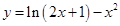 的单调递增区间是 .
的单调递增区间是 .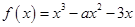
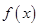 在
在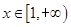 上是增函数,求实数
上是增函数,求实数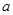 的取值范围;
的取值范围;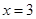 是
是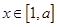 上的最小值和最大值.
上的最小值和最大值.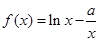 ;
;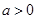 时,判断
时,判断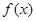 在定义域上的单调性;
在定义域上的单调性;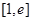 上的最小值.
上的最小值.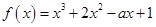 在区间
在区间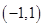 上恰有一个极值点,则实数
上恰有一个极值点,则实数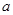 的取值范围是
的取值范围是 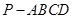 ,
,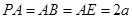 ,
,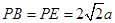 ,
,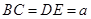 ,
,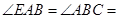
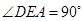 ,
,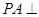 平面
平面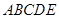 ;
;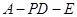 的正弦值.
的正弦值.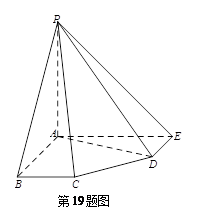
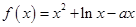 在(0,1)上是增函数.(1)求
在(0,1)上是增函数.(1)求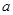 的取值范围;
的取值范围;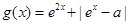 (
(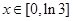 ),试求函数
),试求函数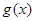 的最小值.
的最小值.