题目内容
【题目】已知函数f（x）=xlnx，g（x）=﹣x2+ax﹣2．
（1）若曲线f（x）=xlnx在x=1处的切线与函数g（x）=﹣x2+ax﹣2也相切，求实数a的值；
（2）求函数f（x）在
上的最小值；
（3）证明：对任意的x∈（0，+∞），都有
成立
【答案】（1）3或-1；（2）见解析；（2）见解析.
【解析】试题分析：（1）求出函数的导数，计算
的值，求出切线方程，再利用判别式为零即可的结果；（2）求出函数的导数，通过讨论
的范围，求出函数的单调区间，从而求出
的最小值即可；（3）设
，求出
的导数, 求出的最大值，得到
恒成立，从而证明结论即可.
试题解析：（1）f′（x）=lnx+x
=lnx+1 ，
时，
，
，
故
在 处的切线方程是：
，
联立
，
消去y得：
，
由题意得：
，
解得：
或
；
（2）由（1）得：
，
x∈（0，
）时，
， 递减，
x∈（，+∞）时， 
，
递增，
①0＜t＜t+
≤
，即0＜t≤﹣
时，
f（x）min=f（t+）=（t+）ln（t+），
②0＜t＜＜t+
，即
﹣＜t＜时，
f（x）min=f（）=﹣；
③≤t＜t+
，即
时， f（x）在递增，
；
综上，f（x）min=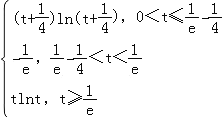
；
（3）证明：设m（x）=
﹣
，（x∈（0，+∞）），则m′（x）=
，
时，
，
递增，
时，
， 递减，
可得m（x）max=m（1）=﹣
，当且仅当 时取到，
由（2）得
，（
）的最小值是﹣，
当且仅当x=时取到，
因此 时，f（x）min≥﹣≥m（x）max恒成立，
又两次最值不能同时取到，
故对任意 ，都有
成立．
【方法点晴】本题主要考查利用导数求曲线切线、利用导数研究函数的单调性以及不等式证明问题，属于难题.求曲线切线方程的一般步骤是：（1）求出
在
处的导数，即在点
出的切线斜率（当曲线在处的切线与
轴平行时，在 处导数不存在，切线方程为）；（2）由点斜式求得切线方程
.
