题目内容
【题目】甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是![]() 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是![]() .假设各局比赛结果相互独立.
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)详见解析;
;(2)详见解析;
【解析】试题分析:(1)甲队获胜有三种情形: ![]() ,
, ![]() ,
, ![]() ,其每种情形的最后一局肯定是甲队获胜,粉笔求出相应的概率,即可得到结果;(2)
,其每种情形的最后一局肯定是甲队获胜,粉笔求出相应的概率,即可得到结果;(2)![]() 的取值可能为
的取值可能为![]() ,然后利用相互独立事件的概率乘法公式求解相应的概率,列出分布列,最后根据期望的公式即可求解数学期望.
,然后利用相互独立事件的概率乘法公式求解相应的概率,列出分布列,最后根据期望的公式即可求解数学期望.
试题解析:(1)记“甲队以3∶0胜利”为事件A1,“甲队以3∶1胜利”为事件A2,
“甲队以3∶2胜利”为事件A3,
由题意知,各局比赛结果相互独立,
故P(A1)=![]() ,
,
P(A2)=![]() ,
,
P(A3)=![]() .
.
所以甲队以3∶0胜利、以3∶1胜利的概率都为![]() ,以3∶2胜利的概率为
,以3∶2胜利的概率为![]() .
.
(2)设“乙队以3∶2胜利”为事件A4,
由题意知,各局比赛结果相互独立,
所以P(A4)=![]() .
.
由题意知,随机变量X的所有可能的取值为0,1,2,3,
根据事件的互斥性得
P(X=0)=P(A1+A2)=P(A1)+P(A2)=![]() .
.
又P(X=1)=P(A3)=![]() ,
,
P(X=2)=P(A4)=![]() ,
,
P(X=3)=1-P(X=0)-P(X=1)-P(X=2)=![]() ,
,
故X的分布列为
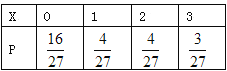
所以E(X)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.

【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.