题目内容
10.已知点A(-3,5)B(0,3),试在直线y=x+1上找一点P,使|PA|+|PB|最小,并求出最小值.分析 求出B(0,3)关于直线y=x+1的对称点B′(2,1),连接AB′交直线y=x+1于P点,此时|PB|+|AP|取最小值|AB′|,由此能求出结果.
解答 解:设B(0,3)关于直线y=x+1的对称点为B′(a,b),
则$\left\{\begin{array}{l}{\frac{b+3}{2}=\frac{a}{2}+1}\\{\frac{b-3}{a}=-1}\end{array}\right.$,解得a=2,b=1,
∴B′(2,1),连接AB′交直线y=x+1于P点,
此时|PB|+|AP|取最小值|AB′|=$\sqrt{(2+3)^{2}+(1-5)^{2}}$=$\sqrt{41}$.
直线AB′的斜率k=$\frac{5-1}{-3-2}$=-$\frac{4}{5}$,
直线AB′的方程:y-1=-$\frac{4}{5}$(x-2),即4x+5y-13=0,
解方程组$\left\{\begin{array}{l}{y=x+1}\\{4x+5y-13=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{8}{9}}\\{y=\frac{17}{9}}\end{array}\right.$,
∴P($\frac{8}{9}$,$\frac{17}{9}$).
∴直线y=x+1上点P($\frac{8}{9}$,$\frac{17}{9}$)使|PA|+|PB|最小,最小值为$\sqrt{41}$.
点评 本题考查使线段和最小的点的坐标及最小的求法,是中档题,解题时要认真审题,注意对称性、两点间距离公式、直线方程等知识的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知点A(-1,0),B(5,6),P(3,4),且$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,则λ=( )
| A. | 3 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
15.将-1485°化成α+2kπ(0≤α<2π,k∈Z)的形式是( )
| A. | -$\frac{π}{4}$-8π | B. | $\frac{7π}{4}$-8π | C. | $\frac{π}{4}$-10π | D. | $\frac{7π}{4}$-10π |
19.下列函数中,既是偶函数,又在区间(0,1)上是增函数的是( )
| A. | y=1+$\frac{1}{|x|}$ | B. | y=||x|-1| | C. | y=($\frac{1}{3}$)-|x| | D. | y=lg(1-x2) |
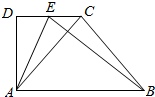 如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,E为CD中点,AB=2CD=4,若$\overrightarrow{AE}$•$\overrightarrow{BE}$=4,则$\overrightarrow{AC}$•$\overrightarrow{BC}$=3.
如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,E为CD中点,AB=2CD=4,若$\overrightarrow{AE}$•$\overrightarrow{BE}$=4,则$\overrightarrow{AC}$•$\overrightarrow{BC}$=3.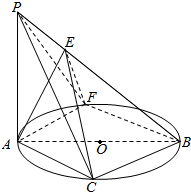 如图,AB是圆O的直径,PA垂直圆O所在的平面,点C,F分别在两个半圆弧的中点,PE∥AC,PA=AC=2,PE=1.
如图,AB是圆O的直径,PA垂直圆O所在的平面,点C,F分别在两个半圆弧的中点,PE∥AC,PA=AC=2,PE=1.