题目内容
1.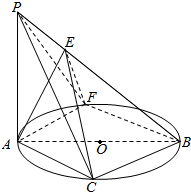 如图,AB是圆O的直径,PA垂直圆O所在的平面,点C,F分别在两个半圆弧的中点,PE∥AC,PA=AC=2,PE=1.
如图,AB是圆O的直径,PA垂直圆O所在的平面,点C,F分别在两个半圆弧的中点,PE∥AC,PA=AC=2,PE=1.(1)求证:BC⊥AE;
(2)求直线PF与平面ECB所成角θ的正弦值.
分析 (1)证明BC⊥平面PAC,即可证明BC⊥AE;
(2)建立如图所示的坐标系,求出平面ECB的平面角,$\overrightarrow{PF}$,即可求直线PF与平面ECB所成角θ的正弦值.
解答 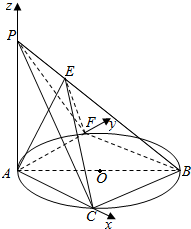 (1)证明:∵AB是圆O的直径,
(1)证明:∵AB是圆O的直径,
∴BC⊥AC,
∵PA垂直圆O所在的平面,
∴PA⊥BC,
∵PA∩AC=A,
∴BC⊥平面PAC,
∵PE∥AC,
∴AE?平面PAC,
∴BC⊥AE;
(2)解:∵点C,F分别在两个半圆弧的中点,
∴AF⊥AC,
建立如图所示的坐标系,则P(0,0,2),F(0,2,0),C(2,0,0),B(2,2,0),E(1,0,2),
设平面ECB的平面角为$\overrightarrow{n}$=(x,y,z),则
∵$\overrightarrow{EC}$=(1,0,-2),$\overrightarrow{EB}$=(1,2,-2),
∴$\left\{\begin{array}{l}{x-2z=0}\\{x+2y-2z=0}\end{array}\right.$,
∴取$\overrightarrow{n}$=(2,0,1),
∵$\overrightarrow{PF}$=(0,2,-2),
∴直线PF与平面ECB所成角θ的正弦值|$\frac{-2}{\sqrt{4+1}•\sqrt{4+4}}$|=$\frac{\sqrt{10}}{10}$.
点评 本题考查线面垂直的性质与判定,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.设a=log36,b=2-2,c=log${\;}_{\frac{1}{2}}$2,则( )
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
10.设a,b是实数,命题“?ab>0,都有a>0,b>0”的否定是( )
| A. | ?ab≤0,使得a≤0,b≤0 | B. | ?ab≤0,使得a≤0或b≤0 | ||
| C. | ?ab>0,使得a≤0,b≤0 | D. | ?ab>0,使得a≤0或b≤0 |