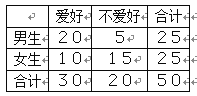
题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知直线
轴正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并指出该曲线是什么曲线;
的直角坐标方程,并指出该曲线是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() .
.
【答案】(1)![]() ,曲线
,曲线![]() 表示焦点坐标为
表示焦点坐标为![]() ,对称轴为
,对称轴为![]() 轴的抛物线.(2)10
轴的抛物线.(2)10
【解析】分析:(1)直接利用转换关系,把参数方程和极坐标方程与直角坐标方程进行转化.
(2)利用直线和曲线的位置关系,建立方程组,利用根和系数的关系求出结果.
详解:(1)因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以曲线![]() 表示焦点坐标为
表示焦点坐标为![]() ,对称轴为
,对称轴为![]() 轴的抛物线.
轴的抛物线.
(2)直线![]() 过抛物线的焦点
过抛物线的焦点![]() ,且参数方程为
,且参数方程为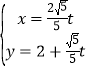 (
(![]() 为参数),
为参数),
代入曲线![]() 的直角坐标方程,得
的直角坐标方程,得![]() ,
,
所以![]() .
.
所以![]() .
.

【题目】为了了解四川省各景点在大众中的熟知度,随机对![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.

组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
| | |
第 |
| | |
第 |
| | |
第 |
| | |
第 |
| | |
(1)分别求出![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() ,
,![]() ,
,![]() 组每组各抽取多少人?
组每组各抽取多少人?
(3)通过直方图求出年龄的众数,平均数.
【题目】为弘扬中华传统文化,学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查,小明同学阅读两类读物的阅读量统计如下:
小明阅读“经典名著”的阅读量![]() (单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
(单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
t | 0 | 10 | 20 | 30 |
| 0 | 2700 | 5200 | 7500 |
阅读“古诗词”的阅读量![]() (单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(单位:字)与时间t(单位:分钟)满足如图1所示的关系.

(1)请分别写出函数![]() 和
和![]() 的解析式;
的解析式;
(2)在每天的一小时课外阅读活动中,小明如何分配“经典名著”和“古诗词”的阅读时间,使每天的阅读量最大,最大值是多少?