题目内容
【题目】如图,三棱维![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上点
上点![]() 是
是![]() 的重心.
的重心.
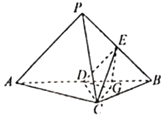
(1)若![]() 是
是![]() 的中点,证明
的中点,证明![]() 面
面![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)详见解析;(2)存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,此时
,此时![]() .
.
【解析】
(1)延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,证明平面
,证明平面![]() 平面
平面![]() ,得到证明.
,得到证明.
(2)证明![]() 平面
平面![]() ,以
,以![]() 为原点建立空间直角坐标系,平面
为原点建立空间直角坐标系,平面![]() 的法向量为
的法向量为 ,平面
,平面![]() 的法向量
的法向量![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,因为点
,因为点![]() 是
是![]() 的重心,故
的重心,故![]() 为
为![]() 的中点,
的中点,
因为![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,![]() ,
,
又因为![]() ,所以平面
,所以平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
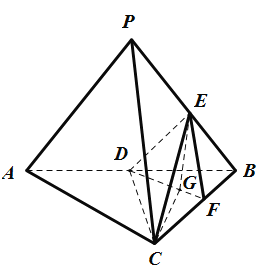
(2)连接![]() ,因为
,因为![]() ,所以
,所以![]() ,又
,又![]() 是
是![]() 的中点,
的中点,
所以![]() ,
,
因为平面![]() 平面
平面![]() ,而平面
,而平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
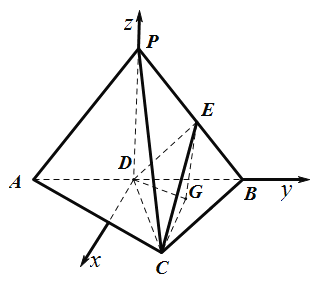
如图,以![]() 为原点,垂直于
为原点,垂直于![]() 的直线为
的直线为![]() 轴,
轴,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴建空间直角坐标系,
轴建空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,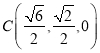 ,
,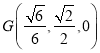 ,
,![]() ,
,
假设存在点![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,
,
所以![]() ,又
,又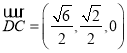 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则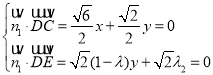 ,
,
令![]() ,解得
,解得 ,
,
又平面![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
而二面角![]() 的大小为
的大小为![]() ,所以
,所以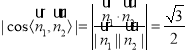 ,
,
即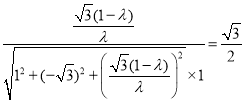 ,解得
,解得![]() ,
,
所以存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,此时
,此时![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
【题目】为了判断英语词汇量与阅读水平是否相互独立,某语言培训机构随机抽取了100位英语学习者进行调查,经过计算![]() 的观测值为7,根据这一数据分析,下列说法正确的是( )
的观测值为7,根据这一数据分析,下列说法正确的是( )
附:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
A.有99%以上的把握认为英语词汇量与阅读水平无关
B.有99.5%以上的把握认为英语词汇量与阅读水平有关
C.有99.9%以上的把握认为英语词汇量与阅读水平有关
D.在犯错误的概率不超过1%的前提下,可以认为英语词汇量与阅读水平有关