题目内容
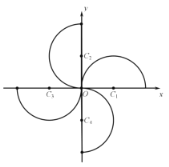
【题目】在直角坐标系
中，曲线
，如图将
分别绕原点
逆时针旋转
，
，
得到曲线
，
，
．以坐标原点为极点，
轴的正半轴为极轴建立极坐标系．
（1）分别写出曲线
的极坐标方程；
（2）设
交
于
两点，
交
于
两点（其中
均不与原点重合），若四边形
的面积为
，求
的值.
【答案】（1）
的极坐标方程为
， 
的极坐标方程为
的极坐标方程为
， 
的极坐标方程为
．
（2）
【解析】
（1）将
代入，得的极坐标方程为
，再利用旋转可得
的极坐标方程；
（2）将
代入得
， 将
代入得
， 再根据面积关系，可求得
的值.
（1）将代入，
得的极坐标方程为，
在
一致的情况下：
点
旋转到点
，且
，所以
，
所以的极坐标方程为
，
点旋转到点，且
，所以
，
所以的极坐标方程为
，
点旋转到点，且
，所以
，
所以的极坐标方程为
．
（2）将代入得，
将代入得，
因为
，
解得
，因为
，所以．
练习册系列答案
相关题目
