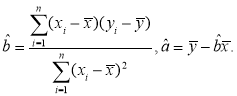题目内容
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)是否存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,若存在,求出实数
,若存在,求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)当![]() 时,
时, ![]() ,对
,对![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)2.
【解析】
(Ⅰ)由![]() ,讨论
,讨论![]() 和
和![]() 导数的正负,从而可得函数的单调性;
导数的正负,从而可得函数的单调性;
(Ⅱ)由正实数a,结合(Ⅰ)的单调性可得![]() ,即g(x)=f(x)+
,即g(x)=f(x)+![]() 在
在![]() 上单调递减,求导可得a
上单调递减,求导可得a![]() 对
对![]() 恒成立,分析不等式右边函数的最值即可;
恒成立,分析不等式右边函数的最值即可;
(Ⅲ)由题意得lnx![]() 对
对![]() 恒成立,当x=1时,b
恒成立,当x=1时,b![]() ; 又 b
; 又 b![]() ,通过证明b=2时不等式成立即可得解.
,通过证明b=2时不等式成立即可得解.
(Ⅰ)∵![]() ,
,![]() .
.
∴(ⅰ)若![]() ,则
,则![]() 恒成立
恒成立![]() f(x)在
f(x)在![]() 上单调递增;
上单调递增;
(ⅱ)若![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() .
.
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上:当![]() 时,f(x)在
时,f(x)在![]() 上单调递增;
上单调递增;
当![]() 时,f(x)在
时,f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)满足条件的a不存在.理由如下:
若![]() ,由(Ⅰ)可知,函数f(x)=alnx+
,由(Ⅰ)可知,函数f(x)=alnx+![]() 在
在![]() 为增函数;
为增函数;
不妨设![]() ,
,
则![]() ,即
,即![]()
∴由题意:g(x)=f(x)+![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 上恒成立,即a
上恒成立,即a![]() 对
对![]() 恒成立;
恒成立;
又![]() 在
在![]() 上单调递减;
上单调递减;
∴a![]() ;故满足条件的正实数a不存在.
;故满足条件的正实数a不存在.
(Ⅲ)当a=1时,使![]() 对
对![]() 恒成立
恒成立
即lnx![]() 对
对![]() 恒成立.
恒成立.
∴ 当x=1时,b![]() ; 又 b
; 又 b![]()
下面证明:当b=2时,lnx![]() 对
对![]() 恒成立.
恒成立.
当b=2时,lnx![]() .
.
设g(x)=![]() ,则
,则![]() .
.
易知:![]()
![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴g(x)![]()
即当b=2时,lnx![]() 对
对![]() 恒成立.∴
恒成立.∴![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】中国共产党第十九次全国代表大会于2017年10月18日至10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚”情况,从某县调查得到农村居民2013年至2017年家庭人均纯收入![]() (单位:百元)的数据如表:
(单位:百元)的数据如表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 47 | 55 | 61 | 65 | 72 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入指标能否达到“全面建成小康社会”的标准?
附:回归直线![]() 斜率和截距的最小二乘估计公式分别为:
斜率和截距的最小二乘估计公式分别为: