题目内容
本小题满分14分)
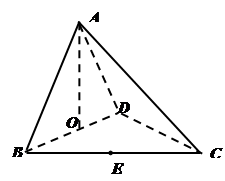
如图,在直三棱柱 中,
中, ,
, ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)证明:平面 平面
平面 ;
;
(Ⅲ)求多面体A1B1C1BD的体积V.
如图,在直三棱柱
 中,
中, ,
, ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点. (Ⅰ)求证:
 平面
平面 ;
; (Ⅱ)证明:平面
 平面
平面 ;
;(Ⅲ)求多面体A1B1C1BD的体积V.

(Ⅰ)证明:见解析(Ⅱ)证明:见解析;
(Ⅲ)V= 。
。
(Ⅲ)V=
 。
。试题分析:(I)根据线面平行的判定定理只需证明:AE//平面BC1D即可.
(II)因为
 ,所以
,所以 ,然后再利用勾股定理证明
,然后再利用勾股定理证明 ,
,从而可证明:
 ,再根据面面垂直的判定定理得平面
,再根据面面垂直的判定定理得平面 平面
平面 .
.(III) 取A1B1中点F,易证:C1F⊥面A1B1BD,从而得到所求四棱锥
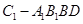 的高,然后再根据棱锥的体积计算公式计算即可.
的高,然后再根据棱锥的体积计算公式计算即可.(Ⅰ)证明:在矩形
 中,
中,由

得
 是平行四边形.…………………1分
是平行四边形.…………………1分所以
 , …………………2分
, …………………2分
又
 平面
平面 ,
, 平面
平面 ,
,所以
 平面
平面 …………………4分
…………………4分(Ⅱ)证明:直三棱柱
 中,
中, ,
, ,
, ,所以
,所以 平面
平面 ,…………………6分
,…………………6分而
 平面
平面 ,所以
,所以
 .…………………7分
.…………………7分在矩形
 中,
中, ,从而
,从而 ,
,所以

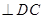 , …………………8分
, …………………8分又
 ,所以
,所以 平面
平面 , …………………9分
, …………………9分而
 平面
平面 ,所以平面
,所以平面 平面
平面 …………………10分
…………………10分(Ⅲ)取A1B1中点F,由A1C1=B1C1知C1F⊥A1B1,……………11分
又直三棱柱中侧面ABA1B1⊥底面A1B1C1且交线为A1B1,故C1F⊥面A1B1BD,……12分
∴V=
 …………………14分
…………………14分点评:掌握线线、线面,面面垂直的判定与性质定理是解决此类证明的关键,并且还要记住柱,锥,台体的体积及表面积公式.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
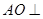 平面BCD;
平面BCD; 、
、 ,直线
,直线 ,若
,若 ,
, ,则
,则 ;④四个侧面两两全等的四棱柱为直四棱柱;⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.其中正确命题的序号是 .
;④四个侧面两两全等的四棱柱为直四棱柱;⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.其中正确命题的序号是 . 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )

 的所成角相等,则
的所成角相等,则
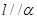
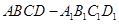 中,
中,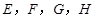 分别为
分别为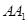 ,
,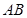 ,
,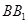 ,
,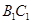 的中点,则异面直线
的中点,则异面直线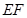 与
与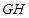 所成的角等于( )
所成的角等于( )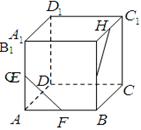
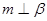 .(填所选条件的序号)
.(填所选条件的序号)  是空间四条直线.如果“
是空间四条直线.如果“ ”,则( )
”,则( ) 且
且
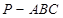 中,
中,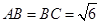 ,平面
,平面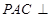 平面
平面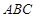 ,
,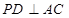 于点
于点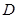 ,
, 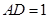 ,
,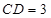 ,
,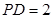 .
.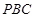 为直角三角形.
为直角三角形.