题目内容
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
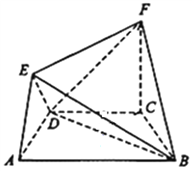
(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
【解析】试题分析:(1)要证线面平行,先找线线平行,先证平面AED⊥平面ABCD,做过E作EG⊥AD于G,则EG⊥平面ABCD,∴FC∥EG,进而得到线面平行;(2)建系,求面的法向量和线的方向向量,根据向量夹角得到线面角,即可。
解析:
(Ⅰ)证明:∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴BC=DC,∠ADC=∠BCD=120°,∴∠CDB=30°,
∴∠ADB=90°,即BD⊥AD.
又AE⊥BD, ![]() =A,∴BD⊥平面AED,
=A,∴BD⊥平面AED,
又BD![]() 平面ABCD,∴平面AED⊥平面ABCD.
平面ABCD,∴平面AED⊥平面ABCD.
如图4,过E作EG⊥AD于G,则EG⊥平面ABCD,
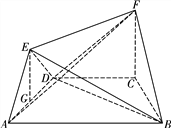
又FC⊥平面ABCD,∴FC∥EG.
又EG![]() 平面AED,FC
平面AED,FC![]() 平面AED,
平面AED,
∴FC∥平面AED.
(Ⅱ)解:如图5,连接AC,由(Ⅰ)知AC⊥BC,
∵FC⊥平面ABCD,
∴CA,CB,CF两两垂直.
以C为原点,建立空间直角坐标系Cxyz.
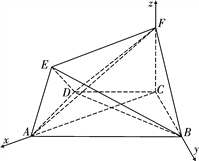
设BC![]() ,则AC
,则AC![]() ,AB
,AB![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,
, ![]() .
.
设平面BDF的法向量为![]() ,
,
则![]() 即
即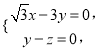
令![]() ,则
,则![]() ,
, ![]() ,则
,则![]() .
.
设直线AF与平面BDF所成角为![]() ,则
,则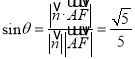 ,
,
故直线AF与平面BDF所成角的余弦值为![]() .
.

练习册系列答案
相关题目

