题目内容
已知函数 =
= ,
,
(1)求函数 的单调区间
的单调区间
(2)若关于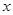 的不等式
的不等式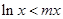 对一切
对一切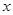
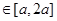 (其中
(其中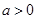 )都成立,求实数
)都成立,求实数 的取值范围;
的取值范围;
(3)是否存在正实数
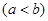 ,使
,使 ?若不存在,说明理由;若存在,求
?若不存在,说明理由;若存在,求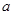 取值的范围
取值的范围
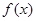 =
=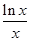 ,
,(1)求函数
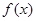 的单调区间
的单调区间(2)若关于
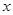 的不等式
的不等式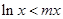 对一切
对一切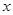
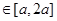 (其中
(其中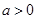 )都成立,求实数
)都成立,求实数 的取值范围;
的取值范围;(3)是否存在正实数

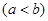 ,使
,使 ?若不存在,说明理由;若存在,求
?若不存在,说明理由;若存在,求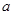 取值的范围
取值的范围(1)单调递增区间是( ),单调递减区间是
),单调递减区间是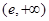 (2)
(2)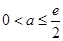 时,
时,
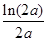 ;
;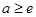 时,
时,
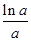 ;
; 时,
时,
 (3)当
(3)当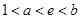 时,
时, ,此时
,此时
 ),单调递减区间是
),单调递减区间是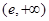 (2)
(2)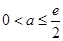 时,
时,
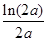 ;
;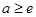 时,
时,
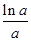 ;
; 时,
时,
 (3)当
(3)当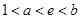 时,
时, ,此时
,此时
试题分析:(1)
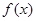 的定义域为
的定义域为 ,
, ,令
,令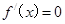 ,得
,得
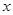 | ( ) ) |  | 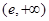 |
 | + | | _ |
 | 增 |  | 减 |
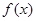 的单调递增区间是(
的单调递增区间是( ),单调递减区间是
),单调递减区间是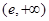 3分
3分(2)∵不等式
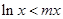 对一切
对一切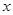
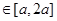 (其中
(其中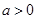 )都成立,
)都成立,∴
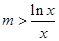 对一切
对一切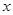
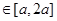 (其中
(其中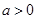 )都成立 即
)都成立 即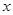
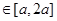 时,
时,
∵
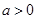
①当
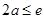 时,即
时,即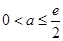 时,
时,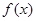 在
在 上单调递增,
上单调递增, =
=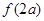 =
=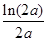
②
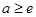 时,
时,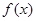 在
在 上单调递减,
上单调递减, =
= =
=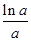
③
 ,即
,即 时,
时,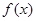 在上
在上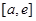 单调递增,
单调递增, 上单调递减,
上单调递减, =
=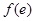 =
=
综上,
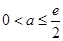 时,
时,
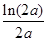 ;
;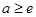 时,
时,
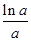 ;
; 时,
时,
 9分
9分(3)存在 10分
 即
即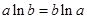 ,
,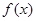 =
=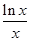 在
在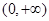 上有两个不同点的函数值相等
上有两个不同点的函数值相等 ∵
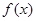 在(
在( )单调递增,在
)单调递增,在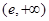 上单调递减
上单调递减 当
 时,
时,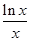
 ,
,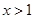 时,
时,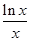
 ,数形结合知
,数形结合知当
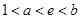 时,
时, ,此时
,此时
点评:求函数单调区间通常利用导数的正负解决,第二问中将不等式恒成立问题转化为函数最值问题,这是常用的转化思路,但要注意分情况讨论得到不同的最值,第三问对于条件指数式将其转化为对数式从而和已知函数发生联系,这种转化学生可能不易想到

练习册系列答案
相关题目
 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当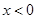 时,
时, ,且g(-3)=0,则不等式
,且g(-3)=0,则不等式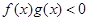 的解集是 ( )
的解集是 ( )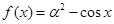 ,则
,则 等于( )
等于( ) 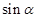

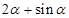

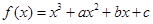 在
在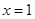 与
与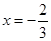 时都取得极值
时都取得极值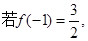 函数f(x)的极值;
函数f(x)的极值;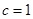 ,方程
,方程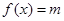 恰好有三个根,求
恰好有三个根,求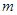 的取值范围.
的取值范围. ,
,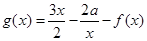 (其中
(其中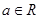 ).
). 的单调区间;
的单调区间;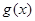 在区间
在区间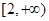 上为增函数,求
上为增函数,求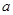 的取值范围;
的取值范围; ,当
,当 时,若存在
时,若存在 ,对任意的
,对任意的 ,总有
,总有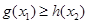 成立,求实数
成立,求实数 的取值范围.
的取值范围.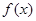 的定义域是
的定义域是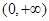 ,
,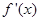 是
是 在
在 的单调区间;
的单调区间;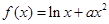 ,求
,求 的取值范围;
的取值范围;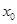 是
是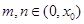 ,求证:
,求证: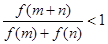
 ,
, ,(
,( ).
). 的极值;
的极值; ,函数
,函数 ,
,  ,判断并证明
,判断并证明 的单调性;
的单调性; ,试比较
,试比较 与
与 ,并加以证明.
,并加以证明. 的最小值为0,其中
的最小值为0,其中 。
。 ,有
,有 成立,求实数k的最小值
成立,求实数k的最小值
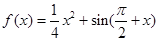 ,
, 为
为 的导函数,则
的导函数,则