题目内容
已知函数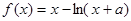 的最小值为0,其中
的最小值为0,其中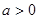 。
。
(1)求a的值
(2)若对任意的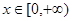 ,有
,有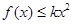 成立,求实数k的最小值
成立,求实数k的最小值
(3)证明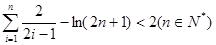
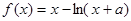 的最小值为0,其中
的最小值为0,其中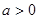 。
。(1)求a的值
(2)若对任意的
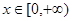 ,有
,有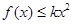 成立,求实数k的最小值
成立,求实数k的最小值(3)证明
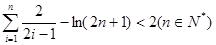
(1) (2)
(2) (3)利用放缩法来证明
(3)利用放缩法来证明
 (2)
(2) (3)利用放缩法来证明
(3)利用放缩法来证明试题分析:(1)
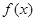 的定义域为
的定义域为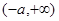
 ,由
,由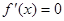 ,得
,得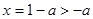 ,
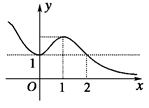
,当x变化时,
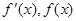 的变化情况如下表:
的变化情况如下表:| x |  |  | 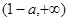 |
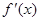 | - | 0 | + |
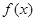 | ↘ | 极小值 | ↗ |
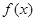 在
在 处取得最小值,故由题意
处取得最小值,故由题意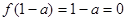 ,所以
,所以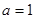 。
。(Ⅱ)解:当
 时,取
时,取 ,有
,有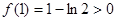 ,故
,故 不合题意。
不合题意。当
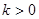 时,令
时,令 ,即
,即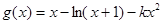 。
。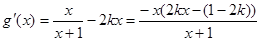 ,令
,令 ,得
,得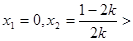
-1。
(1) 当
 时,
时,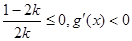 在
在 上恒成立,因此
上恒成立,因此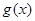 在
在 上单
上单调
(2) 递减,从而对于任意的
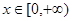 ,总有
,总有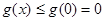 ,即
,即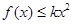 在
在
上恒成立。故
 符合题意。
符合题意。(2)当
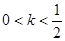 时,
时,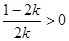 ,对于
,对于 ,
,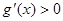 ,故
,故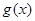 在
在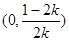 内单调递增,因此当取
内单调递增,因此当取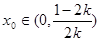 时,
时,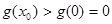 ,即
,即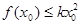 不成立。
不成立。故
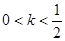 不合题意,
不合题意,综上,k的最小值为
 。
。(Ⅲ)证明:当n=1时,不等式左边
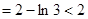 =右边,所以不等式成立。
=右边,所以不等式成立。当
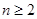 时,
时,
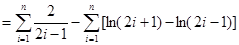
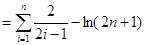 。
。在(Ⅱ)中取
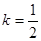 ,得
,得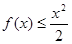
 ,从而
,从而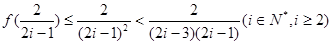 ,
,所以有

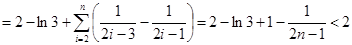 。
。综上,
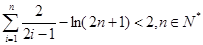 。
。点评:本题考查恒成立问题,第二问构造新函数,将问题转化为g(x)的最大值小于等于0,
即可,这种转化的思想在高考中经常会出现,我们要认真体会.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
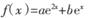 (a ,b
(a ,b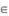 R,e为自然对数的底数),
R,e为自然对数的底数),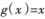 .
.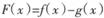 存在单调递增区间,求a的取值范围;
存在单调递增区间,求a的取值范围;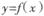 的图象C1与
的图象C1与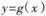 的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点
的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点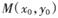 ,求证
,求证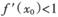 .
.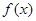 =
=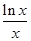 ,
,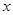 的不等式
的不等式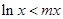 对一切
对一切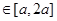 (其中
(其中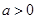 )都成立,求实数
)都成立,求实数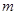 的取值范围;
的取值范围;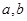
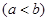 ,使
,使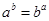 ?若不存在,说明理由;若存在,求
?若不存在,说明理由;若存在,求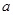 取值的范围
取值的范围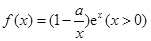 ,其中
,其中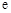 为自然对数的底数.
为自然对数的底数.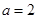 时,求曲线
时,求曲线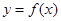 在
在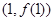 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;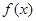 存在一个极大值和一个极小值,且极大值与极小值的积为
存在一个极大值和一个极小值,且极大值与极小值的积为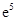 ,求
,求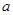 的
的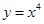 的一条切线
的一条切线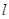 与直线
与直线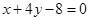 垂直,则
垂直,则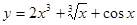 ,则导数
,则导数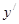 =( )
=( )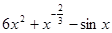
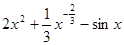
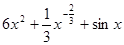

 上的奇函数
上的奇函数 ,若
,若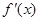 满足
满足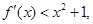 则不等式
则不等式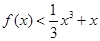 的解集为( )
的解集为( )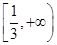

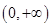
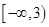
 在R上满足
在R上满足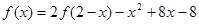 ,则曲线
,则曲线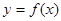
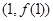 处的切线方程是 .
处的切线方程是 .