题目内容
17.双曲线${x^2}-\frac{y^2}{4}=1$的左焦点F,到其中一条渐近线的距离为2.分析 求得双曲线的a,b,c,焦点F的坐标和一条渐近线方程,由点到直线的距离公式计算即可得到所求.
解答 解:双曲线${x^2}-\frac{y^2}{4}=1$的a=1,b=2,c=$\sqrt{5}$,
左焦点F为(-$\sqrt{5}$,0),
一条渐近线方程为y=-2x,
则F到渐近线的距离为d=$\frac{|2\sqrt{5}|}{\sqrt{1+4}}$=2.
故答案为:2.
点评 本题考查双曲线的方程和性质,主要考查渐近线方程的运用,点到直线的距离公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是( )
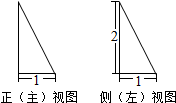

| A. | $\frac{1}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2}{3}$ | D. | 1 |
12.平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=7,∠CBA=120°,∠BAA1=∠DAA1=45°,则AC1的长等于( )
| A. | 83 | B. | $\sqrt{83}$ | C. | 98$+56\sqrt{2}$ | D. | $\sqrt{98+56\sqrt{2}}$ |
2.给出两个命题:命题p:命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0”;命题q:函数y=log2($\sqrt{{x}^{2}+1}$-x)是奇函数.则下列命题是真命题的是( )
| A. | p∧q | B. | p∨¬q | C. | p∨q | D. | p∧¬q |
9.某空间几何体的三视图如图所示,则此几何体的体积为( )
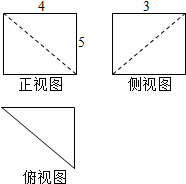

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |