题目内容
2.给出两个命题:命题p:命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0”;命题q:函数y=log2($\sqrt{{x}^{2}+1}$-x)是奇函数.则下列命题是真命题的是( )| A. | p∧q | B. | p∨¬q | C. | p∨q | D. | p∧¬q |
分析 由含量词的命题的否定和函数的奇偶性分别可判p假q真,由复合命题的真假可得.
解答 解:∵命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,∴命题p为假;
又函数y=log2($\sqrt{{x}^{2}+1}$-x)定义域为R,且log2($\sqrt{{x}^{2}+1}$+x)+log2($\sqrt{{x}^{2}+1}$-x)=log21=0,
∴log2($\sqrt{{x}^{2}+1}$+x)=-log2($\sqrt{{x}^{2}+1}$-x),∴函数是奇函数,命题q为真.
由复合命题的真假结合选项可得C正确.
故选:C.
点评 本题考查复合命题的真假,涉及含量词的命题的否定和函数的奇偶性,属基础题.

练习册系列答案
相关题目
14.已知集合A={0,1,2,3},B={1,3},则A∩B=( )
| A. | {1} | B. | {3} | C. | {1,3} | D. | {0,1,2,3} |
11.不等式(a2-4)x2+(a+2)x-1≥0的解集是空集,则实数a的范围为( )
| A. | $(-2,\frac{6}{5})$ | B. | $[-2,\frac{6}{5})$ | C. | $[-2,\frac{6}{5}]$ | D. | $[-2,\frac{6}{5})∪\{2\}$ |
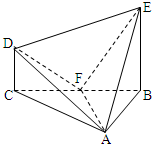 在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,设F是BC的中点.
在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,设F是BC的中点.