题目内容
7.已知数列{an}的通项公式为an=nsin$\frac{nπ}{2}$+1,前n项和为Sn,则S2015=-2014.分析 an=nsin$\frac{nπ}{2}$+1,可得a1=2,a2=1,a3=-3+1=-2,a4=1,a5=5+1=6,…,于是a2k=2ksinkπ+1=1,a2k-1=(2k-1)$sin\frac{2k-1}{2}π$+1=(-1)k+1(2k-1)+1.即可得出.
解答 解:∵an=nsin$\frac{nπ}{2}$+1,
∴a1=2,a2=1,a3=-3+1=-2,a4=1,a5=5+1=6,…,
可得a2k=2ksinkπ+1=1,a2k-1=(2k-1)$sin\frac{2k-1}{2}π$+1=(-1)k+1(2k-1)+1.
∴S2015=(a1+a3+…+a2015)+(a2+a4+…+a2014)
=[(1-3)+(5-7)+…+(2011-2013)-2015+1008]+1007
=(-2×1007-2015+1008)+1007
=-2014.
故答案为:-2014.
点评 本题考查了递推关系的应用、分组求和问题、三角函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.若点(x1,y1)、(x2,y2)、(x3,y3)都是反比例函数$y=-\frac{1}{x}$图象上的点,且x1<0<x2<x3,则下列各式中正确的是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
16.一个几何体的三视图如图所示,则这个几何体的体积为( )
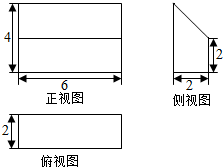

| A. | 9 | B. | 10 | C. | 36 | D. | 72 |