题目内容
(本小题满分12分)
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面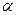 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在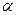 的上侧,分别以△
的上侧,分别以△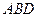 与△
与△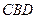 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(1)求证:PQ⊥BD;
(2)求点P到平面QBD的距离.
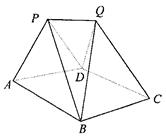
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面
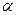 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在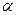 的上侧,分别以△
的上侧,分别以△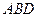 与△
与△ 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.(1)求证:PQ⊥BD;
(2)求点P到平面QBD的距离.

解:(1)由P-ABD,Q-CBD是相同正三棱锥,可知
△PBD与△QBD是全等等腰△.取BD中点E,
连结PE、QE,则BD⊥PE,BD⊥QE.故BD⊥平面PQE,
从而BD⊥PQ.
(2)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则
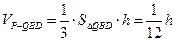
 ∴
∴ 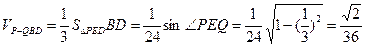 .
.
∴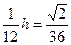 . ∴
. ∴ 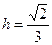 .
.
△PBD与△QBD是全等等腰△.取BD中点E,
连结PE、QE,则BD⊥PE,BD⊥QE.故BD⊥平面PQE,
从而BD⊥PQ.
(2)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则
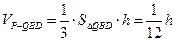
 ∴
∴ 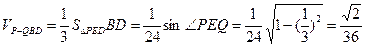 .
.∴
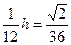 . ∴
. ∴ 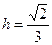 .
.略

练习册系列答案
相关题目
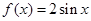 图象按向量
图象按向量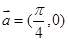 平移得函数
平移得函数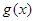 的图象,则函数
的图象,则函数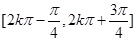 (
(  )
)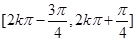 (
(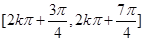 (
(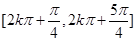 (
(
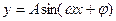 (
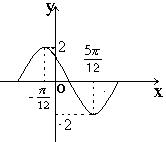
(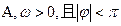 )在一个周期内的图象如右图,
)在一个周期内的图象如右图, )
)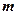
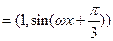 ,
,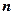
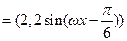 (其中
(其中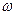 为正常数)
为正常数)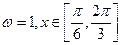 ,求
,求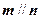 时
时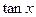 的值;
的值;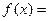
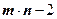 ,若函数
,若函数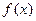 的图像的相邻两个对称中心的距离为
的图像的相邻两个对称中心的距离为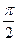 ,求
,求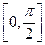 上的最小值。
上的最小值。 角
角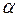 是第三象限角,且
是第三象限角,且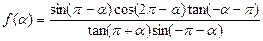
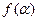 ;
;  2)若
2)若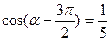 ,求
,求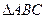 中,角
中,角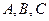 的对边分别为
的对边分别为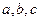 .
. 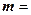
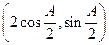 ,
,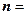
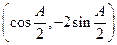 ,.
,.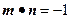
 的值;
的值;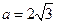 ,
, 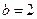 , 求
, 求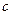 的值.
的值. 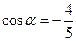 ,且
,且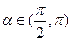 ,则
,则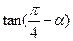 等于 ( )
等于 ( )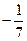
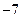

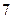
 BC中,a、b、c分别是角A、B、C的对边,
BC中,a、b、c分别是角A、B、C的对边,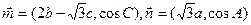 ,
,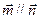 .
.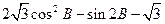 的取值区间。
的取值区间。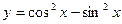 的周期是___________
的周期是___________