Question

【题目】已知复数z1= +（a2﹣3）i，z2=2+（3a+1）i（a∈R，i是虚数单位）．
（1）若复数z1﹣z2在复平面上对应点落在第一象限，求实数a的取值范围；
（2）若虚数z1是实系数一元二次方程x2﹣6x+m=0的根，求实数m值．

Answer 1

【答案】
（1）解：由条件得，z1﹣z2=（ -2）+（a2﹣3a﹣4）i

因为z1﹣z2在复平面上对应点落在第一象限，故有

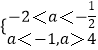∴ 解得﹣2＜a＜﹣1

（2）解：因为虚数z1是实系数一元二次方程x2﹣6x+m=0的根

所以z1+ = =6，即a=﹣1，

把a=﹣1代入，则z1=3﹣2i， =3+2i，）

所以m=z1 =13

【解析】（1）由题设条件，可先通过复数的运算求出的代数形式的表示，再由其几何意义得出实部与虚部的符号，转化出实数a所满足的不等式，解出其取值范围；（2）实系数一元二次方程x2﹣6x+m=0的两个根互为共轭复数，利用根与系数的关系求出a的值，从而求出m的值．
【考点精析】本题主要考查了复数的定义的相关知识点，需要掌握形如的数叫做复数，和分别叫它的实部和虚部才能正确解答此题．