题目内容
【题目】如果函数f(x)= ![]() (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[ ![]() ,2]上单调递减,那么mn的最大值为( )
,2]上单调递减,那么mn的最大值为( )
A.16
B.18
C.25
D.![]()
【答案】B
【解析】解:∵函数f(x)= ![]() (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[ ![]() ,2]上单调递减,∴f′(x)≤0,故(m﹣2)x+n﹣8≤0在[
,2]上单调递减,∴f′(x)≤0,故(m﹣2)x+n﹣8≤0在[ ![]() ,2]上恒成立.而(m﹣2)x+n﹣8是一次函数,在[
,2]上恒成立.而(m﹣2)x+n﹣8是一次函数,在[ ![]() ,2]上的图象是一条线段.故只须在两个端点处f′(
,2]上的图象是一条线段.故只须在两个端点处f′( ![]() )≤0,f′(2)≤0即可.即
)≤0,f′(2)≤0即可.即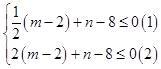
由(2)得m≤ ![]() (12﹣n),
(12﹣n),
∴mn≤ ![]() n(12﹣n)≤
n(12﹣n)≤ ![]()
![]() =18,当且仅当m=3,n=6时取得最大值,经检验m=3,n=6满足(1)和(2).
=18,当且仅当m=3,n=6时取得最大值,经检验m=3,n=6满足(1)和(2).
故选:B.
解法二:
∵函数f(x)= ![]() (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[ ![]() ,2]上单调递减,
,2]上单调递减,
∴①m=2,n<8
对称轴x=﹣ ![]() ,
,
② 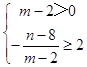 即
即 ![]()
③ 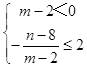 即
即 ![]()
设 ![]() 或
或 ![]() 或
或 ![]()
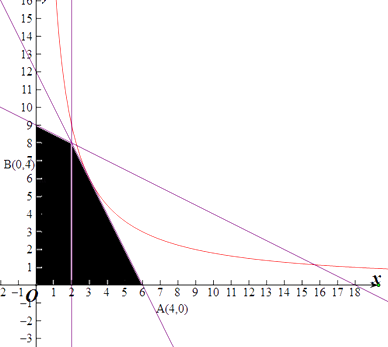
设y= ![]() ,y′=
,y′= ![]() ,
,
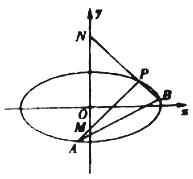
当切点为(x0 , y0),k取最大值.
①﹣ ![]() =﹣2.k=2x
=﹣2.k=2x ![]() ,
,
∴y0=﹣2x0+12,y0= ![]() =2x0 , 可得x0=3,y0=6,
=2x0 , 可得x0=3,y0=6,
∵x=3>2
∴k的最大值为3×6=18
②﹣ ![]() =﹣
=﹣ ![]() ,k=
,k= ![]() ,
,
y0= ![]() =
= ![]() ,
,
2y0+x0﹣18=0,
解得:x0=9,y0= ![]()
∵x0<2
∴不符合题意.
③m=2,n=8,k=mn=16
综合得出:m=3,n=6时k最大值k=mn=18,
故选:B
【考点精析】本题主要考查了二次函数的性质和函数的极值与导数的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;求函数
上递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示. 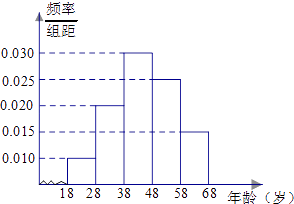
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.