题目内容
【题目】设不等式组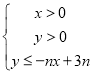 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
【答案】(1)f(1)=3,f(2)=6,f(n)=3n(2)Sn=6+(3n-3)2n+1(3)![]()
【解析】
试题分析:(1)由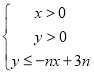 ,可求得x=1,或x=2,则Dn内的整点在直线x=1和x=2上,联立可求得整点纵坐标,进而可得整点个数;(2)利用错位相减法求数列
,可求得x=1,或x=2,则Dn内的整点在直线x=1和x=2上,联立可求得整点纵坐标,进而可得整点个数;(2)利用错位相减法求数列![]() 的前n项的和
的前n项的和![]() ;(3)先利用上面的结论求出
;(3)先利用上面的结论求出![]() 的表达式,再对
的表达式,再对![]() 与
与![]() 的作商比较,从而求出
的作商比较,从而求出![]() 中的最大值,即可找到满足
中的最大值,即可找到满足![]() ≤m时对应的实数m的取值范围
≤m时对应的实数m的取值范围
试题解析:(1)f(1)=3…
f(2)=6……
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n
(2)由题意知:bn=3n·2n
Sn=3·21+6·22+9·23+…+3(n-1)·2n-1+3n·2n
∴2Sn=3·22+6·23+…+3(n-1)·2n+3n·2n+1
∴-Sn=3·21+3·22+3·23+…3·2n-3n·2n+1
=3(2+22+…+2n)-3n·2n+1
=3(2n+1-2)-3nn+1(7分)
∴-Sn=(3-3n)2n+1-6
Sn=6+(3n-3)2n+1
(3)Tn=![]() ………
………
∵![]() …
…
当n=1时![]() >1
>1
当n=2时![]() =1
=1
当n≥3时![]() <1
<1
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3=![]()
∴m≥![]()

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目