题目内容
【题目】已知函数f(x)=ex﹣a+lnx.
(Ⅰ)若a=1,求证:当x>1时,f(x)>2x﹣1;
(Ⅱ)若存在x0≥e,使f(x0)<2lnx0 , 求实数a的取值范围.
【答案】解:(Ⅰ)证明:a=1时, ![]() ,
,
设 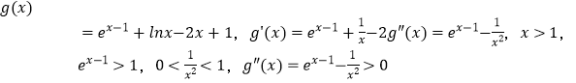 ,g'(x)在(1,+∞)递增,又g'(1)=0,∴x>1时g'(x)>0,g(x)在(1,+∞)递增,
,g'(x)在(1,+∞)递增,又g'(1)=0,∴x>1时g'(x)>0,g(x)在(1,+∞)递增,
x>1时,g(x)>g(1)=0,即ex+lnx﹣2x+1>0,
x>1时,ex+lnx>2x﹣1,即f(x)>2x﹣1….
(Ⅱ)若存在x0≥e,使f(x0)<2lnx0,即 ![]()
即存在x0≥e,使 ![]() .
.
设 ![]() (x≥e),则
(x≥e),则 ![]() ,
,
设 ![]() ,
, ![]() 在[e,+∞)递增,
在[e,+∞)递增,
![]() ,所以u>0在[e,+∞)恒成立,h'(x)>0在[e,+∞)恒成立,
,所以u>0在[e,+∞)恒成立,h'(x)>0在[e,+∞)恒成立,
所以h(x)在[e,+∞)递增,所以x≥e时, ![]() ,
,
需ea>eea>e….
【解析】(1)a=1时,化简求出导数,设![]() ,
,![]() ,然后求解二次导数,求出导函数的最值,然后证明结论;(2)若存在x0≥e,使f(x0)<2lnx0,即
,然后求解二次导数,求出导函数的最值,然后证明结论;(2)若存在x0≥e,使f(x0)<2lnx0,即![]() ,即存在
,即存在![]() ,使
,使![]() ,设
,设![]() ,求出导函数,设
,求出导函数,设![]() ,通过函数的单调性求解函数的最值,推出结果,
,通过函数的单调性求解函数的最值,推出结果,
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值与导数(求函数
在这个区间单调递减),还要掌握函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值)的相关知识才是答题的关键.
是极小值)的相关知识才是答题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
质量指标值m | m<185 | 185≤m<205 | M≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?