题目内容
【题目】如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BCAE=DCAF,B,E,F,C四点共圆.证明:CA是△ABC外接圆的直径.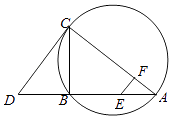
【答案】证明:∵B,E,F,C四点共圆,∴∠DBC=∠EAF.
∵CD为△ABC外接圆的切线,∴∠BCD=∠FAE.
在△BCD与△FAE中,
∵BCAE=DCAF,即 ![]() =
= ![]() ,又∠BCD=∠FAE.
,又∠BCD=∠FAE.
∴△BCD∽△FAE,
∴∠DBC=∠EFA.
∴∠DBC=∠CBA,
又∠DBC+∠CBA=180°,
∴∠CBA=90°.
∴CA是△ABC外接圆的直径.
【解析】先证明△BCD∽△FAE,进而可证∠DBC=∠CBA,从而可证∠CBA=90°,即可证CA是△ABC外接圆的直径.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目