题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 且
且![]() ,点
,点![]() 在椭圆内部,点
在椭圆内部,点![]() 在椭圆上,则以下说法正确的是( )
在椭圆上,则以下说法正确的是( )
A.![]() 的最小值为
的最小值为![]()
B.椭圆![]() 的短轴长可能为2
的短轴长可能为2
C.椭圆![]() 的离心率的取值范围为
的离心率的取值范围为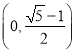
D.若![]() ,则椭圆
,则椭圆![]() 的长轴长为
的长轴长为![]()
【答案】ACD
【解析】
A. 将![]() ,利用椭圆的定义转化为
,利用椭圆的定义转化为![]() 求解;
求解;
B.假设椭圆![]() 的短轴长为2,则
的短轴长为2,则![]() ,与点
,与点![]() 在椭圆的内部验证;
在椭圆的内部验证;
C. 根据点![]() 在椭圆内部,得到
在椭圆内部,得到![]() ,又
,又![]() ,解得
,解得![]() ,再由
,再由![]() 求解;
求解;
D. 根据![]() ,得到
,得到![]() 为线段
为线段![]() 的中点,求得
的中点,求得![]() 坐标,代入椭圆方程求解.
坐标,代入椭圆方程求解.
A. 因为![]() ,所以
,所以![]() ,所以
,所以![]() ,当
,当![]() ,三点共线时,取等号,故正确;
,三点共线时,取等号,故正确;
B.若椭圆![]() 的短轴长为2,则
的短轴长为2,则![]() ,所以椭圆方程为
,所以椭圆方程为![]() ,
,![]() ,则点
,则点![]() 在椭圆外,故错误;
在椭圆外,故错误;
C. 因为点![]() 在椭圆内部,所以
在椭圆内部,所以![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得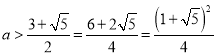 ,所以
,所以![]() ,所以
,所以![]() ,所以椭圆
,所以椭圆![]() 的离心率的取值范围为
的离心率的取值范围为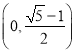 ,故正确;
,故正确;
D. 若![]() ,则
,则![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() ,又
,又![]() ,即
,即![]() ,解得
,解得 ,所以
,所以![]() ,所以椭圆
,所以椭圆![]() 的长轴长为
的长轴长为![]() ,故正确.
,故正确.
故选:ACD

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目