题目内容
8.已知函数y=f(x)是R上的奇函数,且x>0时,f(x)=lg(2x),若g(x)=sinπx,则函数y=f(x)与y=g(x)图象公共点的个数为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 先求出g(x)的周期,并知道f(5)=1,从而x>5时,f(x)和g(x)便没有公共点了,这样画出f(x),g(x)在x正半轴的图象,由图象便可看出在x正半轴f(x),g(x)的公共点个数,根据f(x),g(x)都关于原点对称,从而在x负半轴f(x),g(x)公共点个数等于在正半轴的公共点个数,并容易看出原点是f(x),g(x)的公共点,这样即可得出f(x),g(x)图象的公共点个数.
解答 解:g(x)的周期为2,且x=5时,f(5)=1,x=$\frac{1}{2}$时,f($\frac{1}{2}$)=0;
∴画出x>0时f(x)和g(x)的图象: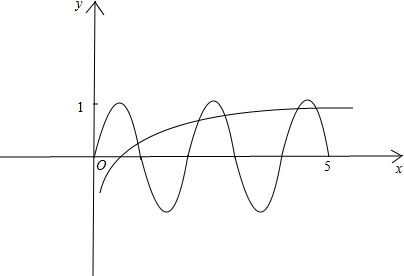 由图象可看出x>0时,f(x)与g(x)的图象有5个公共点;
由图象可看出x>0时,f(x)与g(x)的图象有5个公共点;
据f(x),g(x)都为奇函数,
∴f(x),g(x)的图象都关于原点O对称;
∴x>0时f(x),g(x)的5个公共点关于原点的对称点便是x负半轴的f(x),g(x)图象的公共点;
又(0,0)∈f(x),(0,0)∈g(x),即原点是f(x),g(x)的公共点;
∴函数y=f(x)与y=g(x)图象公共点的个数为11.
故选D.
点评 考查函数y=Asin(ωx+φ)的周期公式及其值域,数形结合解题的方法,奇函数图象的对称性,奇函数f(x)在原点有定义时,f(0)=0.

练习册系列答案
相关题目
20.已知X和Y是两个分类变量,由公式K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$算出K2的观测值k约为7.822根据下面的临界值表可推断( )
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 推断“分类变量X和Y没有关系”犯错误的概率上界为0.010 | |
| B. | 推断“分类变量X和Y有关系”犯错误的概率上界为0.010 | |
| C. | 有至少99%的把握认为分类变量X和Y没有关系 | |
| D. | 有至多99%的把握认为分类变量X和Y有关系 |
19.已知△ABC的三边长分别为a,b,c,若(b+c+a)(b+c-a)=3bc,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
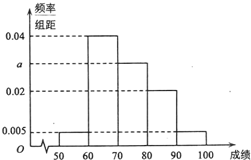 某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].