题目内容
16.已知平面向量$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(x2-1,x+1),(x∈R).(1)若$\overrightarrow{a}⊥\overrightarrow{b}$,求x的值;
(2)若$\overrightarrow{a}∥\overrightarrow{b}$,求|$\overrightarrow{a}-\overrightarrow{b}$|
分析 (1)由已知向量垂直得到数量积为0,得到关于x的等式解出x;
(2)由已知向量平行,得到坐标的关系,求出x,然后求$\overrightarrow{a}-\overrightarrow{b}$的坐标,再求模.
解答 解:(1)因为$\overrightarrow{a}⊥\overrightarrow{b}$,
所以$\overrightarrow{a}•\overrightarrow{b}$=x2-1+3x+3=0,
即x2+3x+2=0,解得x=-1或x=-2;
(2)因为$\overrightarrow{a}∥\overrightarrow{b}$,
所以x+1=3x2-3,解得x=-1或x=$\frac{4}{3}$,
所以$\overrightarrow{b}$=(0,0)或者$\overrightarrow{b}$=($\frac{7}{9}$,$\frac{7}{3}$),
所以$\overrightarrow{a}-\overrightarrow{b}$=(1,3),|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{10}$;
或者$\overrightarrow{a}-\overrightarrow{b}$=(-$\frac{2}{9}$,$\frac{2}{3}$),|$\overrightarrow{a}-\overrightarrow{b}$|=$\frac{2\sqrt{10}}{9}$.
点评 本题考查了向量垂直和平行的坐标关系,关键是由垂直或者平行的性质得到关于x的方程解之.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
11.设数列{an}中,已知a1=1,an=$\frac{1}{2{a}_{n-1}}$(n>1),则a2=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2 |
 上的函数
上的函数 满足:①
满足:① ;②
;② ;③当
;③当 时,
时, ,则
,则 、
、 、
、 满足( )
满足( )



 的定义域为( )
的定义域为( ) B.
B.
 D.
D.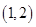
 满足约束条件
满足约束条件 ,则
,则 的最小值等于( )
的最小值等于( ) B.-2 C.
B.-2 C. D.2
D.2