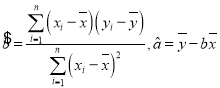题目内容
【题目】已知等差数列{an}的前n项和为Sn，等比数列{bn}的前n项和为Tn，a1＝1，b1＝﹣1，a2-b2＝2.
（1）若a3-b3＝6，求{bn}的通项公式
（2）若T3＝﹣13，求S5.
【答案】(1)
或
；(2)55或﹣15
【解析】
（1）根据等差和等比的基本量，列方程组，即可求得；
（2）根据等比数列前
项和基本量的求解，列出方程，即可求得.
（1）等差数列{an}的公差为d，
等比数列{bn}的公比为q，
由于：a1＝1，b1＝﹣1，a2﹣b2＝2.
所以：（1+d）﹣（﹣1）q＝2 ①
由于a3﹣b3＝6，
则：（1+2d）﹣（﹣1）q2＝6②，
由①②得：q2﹣2q﹣3＝0，
解得：q＝﹣1或3，
故：
或.
（2）由T3＝﹣13，
所以：﹣1+（﹣q）+（﹣q2）＝﹣13，
解得：q＝﹣4或3.
由于：d+q＝5或﹣2.
故：d＝5或﹣2.
①当d＝5时，an＝5n﹣4.
所以S5＝55
②当d＝﹣2时，an＝﹣2n+3，
所以：
.
综上所述：
或
.
练习册系列答案
相关题目
【题目】给出以下命题：①“若x2+ y2 ≠0，则x，y不全为零”的否命题；②“正多边形都相似”的逆命题；③“若m>0，则x2+x-m=0有实根”的逆否命题；其中真命题的序号是____________
【题目】华为公司在2017年8月9日推出的一款手机，已于9月19日正式上市.据统计发现该产品的广告费用x与销售额y的统计数据如下表：
广告费用x（百万元） | 4 | 2 | 3 | 5 |
销售额y（百万元） | 44 | 25 | 37 | 54 |
根据上表可得回归方程
中的
为9.4，据此模型预测广告费用为6百万元时，销售额为（ ）
A.61.5百万元B.62.5百万元C.63.5百万元D.65.0百万元
