题目内容
【题目】在平行四边形ABCD中，A（1，1）、B（7，3）、D（4，6），点M是线段AB的中点线段CM与BD交于点P．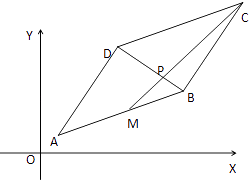 
（1）求直线CM的方程；
（2）求点P的坐标．
【答案】
（1）解：∵ 
，
∴ 
=（7，3）+（4，6）﹣（1，1）=（10，8）．
∴C点坐标C（10，8）．
由中点坐标公式可得：点M坐标（ 
， 
），即（4，2）．
kCM= 
=1，
得出直线CM方程y﹣2=x﹣4，可得：x﹣y﹣2=0
（2）解：kBD= 
=﹣1，
∴BD直线方程y﹣6=﹣（x﹣4），x+y﹣10=0，
联立方程组 
，
解得x=6，y=4，
所以点P坐标为（6，4）
【解析】（1）由 ，可得 ．利用中点坐标公式可得：点M坐标（4，2）．利用斜率计算公式与中点坐标公式即可得出．（2）利用斜率计算公式可得kBD=﹣1，利用点斜式可得BD直线方程，联立解出即可得出．
练习册系列答案
相关题目
