题目内容

【题目】已知椭圆的离心率为，且以原点为圆心，椭圆的焦距为直径的圆与直线相切（为常数）.

（1）求椭圆的标准方程；

（2）如图，若椭圆的左、右焦点分别为，过作直线与椭圆分别交于两点，求的取值范围.

【答案】（1）（2）

【解析】试题分析：（1）由椭圆离心率为，以原点为圆心，椭圆的焦距为直径与直线相切，列出方程组求出的值，由此能求出椭圆的方程；

（2）当直线的斜率不存在时，推导出 ，当直线的斜率存在时，设直线的方程为，联立方程组，利用韦达定理、向量的知识，结合题意，即可求解的取值范围.

试题解析：

（1）由题意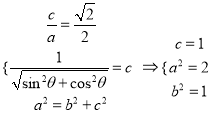

故椭圆.

（2）①若直线斜率不存在，则可得轴，方程为，

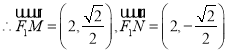，故.

②若直线斜率存在，设直线的方程为，

由消去得，

设，则.

，

则

代入韦达定理可得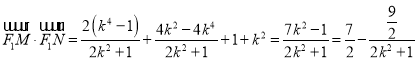

由可得，结合当不存在时的情况，得.

练习册系列答案
相关题目

【题目】已知数列{an}满足an+1=a ﹣nan+1，且a1=2．
（1）计算a2 ， a3 ， a4的值，由此猜想数列{an}的通项公式，并用数学归纳法证明；
（2）求证：2nn≤a ＜3nn ．

【题目】已知函数f（x）=（ + ）x3（a＞0，a≠1）．
（1）讨论函数f（x）的奇偶性；
（2）求a的取值范围，使f（x）+f（2x）＞0在其定义域上恒成立．

【题目】如图为函数图像的一部分，其中点是图像的一个最高点，点是与点相邻的图像与轴的一个交点.

⑴ 求函数的解析式；

⑵ 若将函数的图像沿轴向右平移个单位，再把所得图像上每一点的横坐标都变为原来的（纵坐标不变），得到函数的图像，求函数的单调递增区间.

【题目】如图所示，游乐场中摩天轮匀速逆时针旋转，每转一圈需要6min，其中心距离地面40.5m，摩天轮的半径为40m，已知摩天轮上点P的起始位置在最低点处，在时刻t（min）时点P距离地面的高度为f（t）=Asin（wt+φ）+h（A＞0，w＞0，﹣π＜φ＜0，t≥0）．
（1）求f（t）的单调区间；
（2）求证：f（t）+f（t+2）+f（t+4）是定值．

【题目】如图，正方体ABCD﹣A1B1C1D1中，M、N分别为棱C1D1、C1C的中点，有以下四个结论： ①直线AM与CC1是相交直线；
②直线AM与BN是平行直线；
③直线BN与MB1是异面直线；
④直线AM与DD1是异面直线．
其中正确的结论为（注：把你认为正确的结论的序号都填上）．

【题目】在平行四边形ABCD中，A（1，1）、B（7，3）、D（4，6），点M是线段AB的中点线段CM与BD交于点P．
（1）求直线CM的方程；
（2）求点P的坐标．

【题目】2013年第三季度，国家电网决定对城镇居民用电计费标准作出调整，并根据用电情况将居民分为三类：第一类的用电区间在（0，170]，第二类在（170，260]，第三类在（260，+∞）（单位：千瓦时）．某小区共有1000户居民，现对他们的用电情况进行调查，得到频率分布直方图，如图所示．

（1）求该小区居民用电量的中位数与平均数；
（2）本月份该小区没有第三类的用电户出现，为鼓励居民节约用电，供电部门决定：对第一类每户奖励20元钱，第二类每户奖励5元钱，求每户居民获得奖励的平均值；
（3）利用分层抽样的方法从该小区内选出5位居民代表，若从该5户居民代表中任选两户居民，求这两户居民用电资费属于不同类型的概率．

【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数y与听课时间x（单位：分钟）之间的关系满足如图所示的图象，当x∈（0，12]时，图象是二次函数图象的一部分，其中顶点A（10，80），过点B（12，78）；当x∈[12，40]时，图象是线段BC，其中C（40，50）．根据专家研究，当注意力指数大于62时，学习效果最佳．
（1）试求y=f（x）的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网