题目内容
已知直线 过点
过点 ,圆
,圆 :
: .
.
(1)求截得圆 弦长最长时
弦长最长时 的直线方程;
的直线方程;
(2)若直线 被圆N所截得的弦长为
被圆N所截得的弦长为 ,求直线
,求直线 的方程.
的方程.
解:(1)显然,当直线 通过圆心N时,被截得的弦长最长.………2分
通过圆心N时,被截得的弦长最长.………2分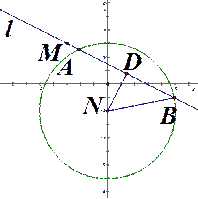
由 ,
, 得
得 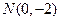
故所求直线 的方程为
的方程为 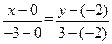
即 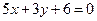 ………4分
………4分
(2)设直线 与圆N交于
与圆N交于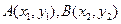 两点(如右图)
两点(如右图)
作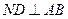 交直线
交直线 于点D,显然D为AB的中点.且有
于点D,显然D为AB的中点.且有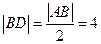 ………6分
………6分
(Ⅰ)若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 
将 代入
代入 ,得
,得
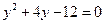
解,得 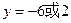 ,
,
因此 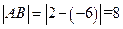 符合题意………8分
符合题意………8分
(Ⅱ)若直线 的斜
的斜 率存在,不妨设直线
率存在,不妨设直线 的方程为
的方程为 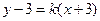 即:
即: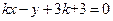
由 ,得
,得 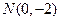 ,
,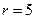
因此 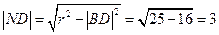 ………10分
………10分
又因为点N到直线 的距离
的距离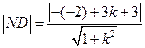
所以 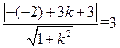 即:
即: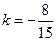
此时 直线 的方程为
的方程为 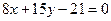
综上可知,直线 的方程为
的方程为 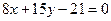 或
或 ………12分
………12分
解析

练习册系列答案
相关题目
椭圆 的焦距是( )
的焦距是( )
| A.3 | B.6 | C.8 | D.10 |
已知双曲线方程为 ,则双曲线的渐近线方程为( ).
,则双曲线的渐近线方程为( ).
A. | B. | C. | D. |
 与圆
与圆 相交于
相交于 两点,
两点, 的取值范围;
的取值范围; 为坐标原点,且
为坐标原点,且 ,求
,求 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线 相切.
相切. 轴相交于
轴相交于
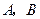 两点,圆内的动点
两点,圆内的动点 使
使 成等比数列,求
成等比数列,求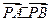 的取值范围(结果用区间表示).:
的取值范围(结果用区间表示).: ,1+
,1+ ),求直线l的方程;
),求直线l的方程; =0,P为圆M上任一点,求
=0,P为圆M上任一点,求 +
+ +
+ 的最值.
的最值. 的所有切线中,求在坐标轴上截距相等的切线方程。
的所有切线中,求在坐标轴上截距相等的切线方程。