ЬтФПФкШн
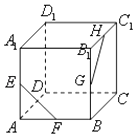
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌABЁЭADЃЌADЁЮBCЃЌADЃН6ЃЌBCЃН2ABЃН4ЃЌEЃЌFЗжБ№дкBCЃЌADЩЯЃЌEFЁЮAB.ЯжНЋЫФБпаЮABCDбиEFелЦ№ЃЌЪЙЦНУцABEFЁЭЦНУцEFDC.
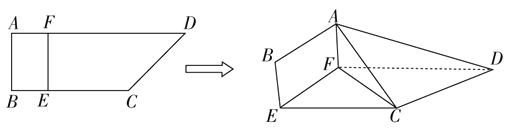
ЃЈЂёЃЉШєBEЃН1ЃЌЪЧЗёдкелЕўКѓЕФЯпЖЮADЩЯДцдквЛЕуPЃЌЧв![]() ЃЌЪЙCPЁЮЦНУцABEFЃПШєДцдкЃЌЧѓГіІЫЕФжЕЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЌЪЙCPЁЮЦНУцABEFЃПШєДцдкЃЌЧѓГіІЫЕФжЕЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈЂђЃЉЧѓШ§РтзЖAЃCDFЕФЬхЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЖўУцНЧEЃACЃFЕФгрЯвжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮі:ЃЈ1ЃЉЙ§ЕуPзїMPЁЮFDНЛAFгкЕуMЃЌШєMP=CE,дђЫФБпаЮMPCEЮЊЦНааЫФБпаЮЃЌМДгаCPЁЮMEЃЌвВОЭЕУCPЁЮЦНУцABEF,вђДЫгЩЯрЫЦБШПЩЕУІЫЕФжЕЃЌЃЈ2ЃЉгЩУцУцДЙжБаджЪЖЈРэЕУAFЁЭЦНУцEFDC,ЫљвдAFЮЊИп,ИљОнШ§РтзЖЬхЛ§ЙЋЪНвдМАЛљБОВЛЕШЪНПЩЕУЬхЛ§зюДѓжЕ;Й§EзїEOЁЭCF,дђИљОнШ§ДЙЯпЖЈРэПЩЕУAOЁЭCF,МДЁЯAOEЮЊЖўУцНЧEЃACЃFЕФЦНУцНЧ,зюКѓЭЈЙ§НтШ§НЧаЮЕУгрЯвжЕ
ЪдЬтНтЮіЃКЁпЦНУцABEFЁЭЦНУцEFDCЃЌЦНУцABEFЁЩЦНУцEFDCЃНEFЃЌFDЁЭEFЃЌ
ЁрFDЁЭЦНУцABEFЃЌгжAFЦНУцABEFЃЌ
ЁрFDЁЭAFЃЌ
дкелЦ№Й§ГЬжаЃЌAFЁЭEFЃЌгжFDЁЩEFЃНFЃЌ
ЁрAFЁЭЦНУцEFDC.
вдFЮЊдЕуЃЌFEЃЌFDЃЌFAЗжБ№ЮЊxЃЌyЃЌzжсНЈСЂПеМфжБНЧзјБъЯЕЃЎ
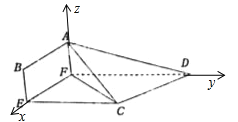 ЃЈIЃЉНтЗЈвЛЃКШєBEЃН1ЃЌдђИїЕузјБъШчЯТЃК
ЃЈIЃЉНтЗЈвЛЃКШєBEЃН1ЃЌдђИїЕузјБъШчЯТЃК
F(0,0,0)ЃЌA(0,0,1)ЃЌD(0,5,0)ЃЌC(2,3,0)ЃЌ
ЁрЦНУцABEFЕФЗЈЯђСППЩЮЊ![]() ЃН(0,5,0)ЃЌ
ЃН(0,5,0)ЃЌ
Ёп![]() ЃНІЫ
ЃНІЫ![]() ЃЌ
ЃЌ
Ёр![]() Ѓ
Ѓ![]() ЃНІЫ(
ЃНІЫ(![]() Ѓ
Ѓ![]() )ЃЌ
)ЃЌ
Ёр![]() ЃН
ЃН![]()
![]() ЃЋ
ЃЋ![]()
![]() ЃН
ЃН![]() (0,0,1)ЃЋ
(0,0,1)ЃЋ![]() (0,5,0)ЃН
(0,5,0)ЃН![]() ЃЌ
ЃЌ
ЁрP![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ШєCPЁЮЦНУцABEFЃЌдђБига![]() ЁЭ
ЁЭ![]() ЃЌМД
ЃЌМД![]() ЁЄ
ЁЄ![]() ЃН0ЃЌ
ЃН0ЃЌ
Ёп![]() ЁЄ
ЁЄ![]() ЃН
ЃН![]() ЁЄ(0,5,0)ЃН
ЁЄ(0,5,0)ЃН![]() ЁЄ5ЃН0ЃЌ
ЁЄ5ЃН0ЃЌ
ЁрІЫЃН![]() ЃЌ
ЃЌ
ЁрADЩЯДцдквЛЕуPЃЌЧв![]() ЃН
ЃН![]()
![]() ЃЌЪЙCPЁЮЦНУцABEF.
ЃЌЪЙCPЁЮЦНУцABEF.
НтЗЈЖўЃКADЩЯДцдквЛЕуPЃЌЪЙCPЁЮЦНУцABEFЃЌДЫЪБІЫЃН![]() .РэгЩШчЯТЃК
.РэгЩШчЯТЃК
ЕБІЫЃН![]() ЪБЃЌ
ЪБЃЌ![]() ЃН
ЃН![]()
![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Й§ЕуPзїMPЁЮFDНЛAFгкЕуMЃЌСЌНгEMЃЌPCЃЌдђга![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
гжBEЃН1ЃЌПЩЕУFDЃН5ЃЌЙЪMPЃН3ЃЌ
гжECЃН3ЃЌMPЁЮFDЁЮECЃЌЙЪгаMPЁЮECЃЌЙЪЫФБпаЮMPCEЮЊЦНааЫФБпаЮЃЌ
ЁрCPЁЮMEЃЌгжCPЦНУцABEFЃЌMEЦНУцABEFЃЌ
ЙЪгаCPЁЮЦНУцABEF.
ЃЈIIЃЉЩшBE
ЙЪVШ§РтзЖAЃCDFЃН![]() ЁЄ
ЁЄ![]() ЁЄ2ЁЄ(6Ѓx)ЁЄxЃН
ЁЄ2ЁЄ(6Ѓx)ЁЄxЃН![]() (Ѓx2ЃЋ6x)ЃЌ
(Ѓx2ЃЋ6x)ЃЌ
ЁрЕБxЃН3ЪБЃЌVШ§РтзЖAЃCDFгазюДѓжЕЃЌЧвзюДѓжЕЮЊ3ЃЌ
ЁрA(0,0,3)ЃЌD(0,3,0)ЃЌC(2,1,0)ЃЌE(2,0,0)ЃЌ
Ёр![]() ЃН(2,0ЃЌЃ3)ЃЌ
ЃН(2,0ЃЌЃ3)ЃЌ![]() ЃН(2,1ЃЌЃ3)ЃЌ
ЃН(2,1ЃЌЃ3)ЃЌ![]() ЃН(0,0,3)ЃЌ
ЃН(0,0,3)ЃЌ![]() ЃН(2,1,0)ЃЌ
ЃН(2,1,0)ЃЌ
ЩшЦНУцACEЕФЗЈЯђСПmЃН(x1ЃЌy1ЃЌz1)ЃЌ
дђ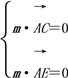 ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Сюx1ЃН3ЃЌдђy1ЃН0ЃЌz1ЃН2ЃЌдђmЃН(3,0,2)ЃЎ
ЩшЦНУцACFЕФЗЈЯђСПnЃН(x2ЃЌy2ЃЌz2)ЃЌ
дђ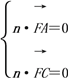 ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Сюx2ЃН1ЃЌдђy2ЃНЃ2ЃЌz2ЃН0ЃЌдђnЃН(1ЃЌЃ2,0)ЃЌ
дђcosЁДmЃЌnЁЕЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЙЪЖўУцНЧEЃACЃFЕФгрЯвжЕЮЊ![]() .
.

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ