题目内容
(本题满分10分)已知函数 是奇函数:
是奇函数:
(1)求实数 和
和 的值; (2)证明
的值; (2)证明 在区间
在区间 上的单调递减
上的单调递减
(3)已知 且不等式
且不等式 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)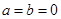 ;(2)
;(2)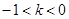 。
。
解析试题分析:(1)由定义易得: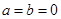 ……2分
……2分
(2)设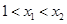 ,
,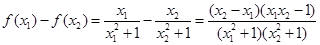
 即
即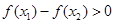 所以
所以 在
在 上的单调递减。……6分
上的单调递减。……6分
(3)已知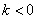 且不等式
且不等式 对任意的
对任意的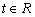 恒成立,求实数
恒成立,求实数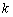 的取值范围.
的取值范围.
由 及
及 为奇函数得:
为奇函数得: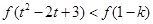
因为 ,
,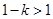 ,且
,且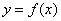 在区间
在区间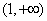 上的单调递减,
上的单调递减,
故 任意的
任意的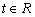 恒成立,故
恒成立,故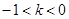 .……10分
.……10分
考点:本题考查奇函数的性质;函数的单调性;单调性、奇偶性与不等式的综合应用。
点评:(1)熟记且灵活应用奇函数的性质:若 是奇函数,且x=0有意义,则f(0)一定为0.(2)利用函数的单调性与奇偶性,将不等式不等式
是奇函数,且x=0有意义,则f(0)一定为0.(2)利用函数的单调性与奇偶性,将不等式不等式 对任意的
对任意的 恒成立,转化为t2-2t+3>1-k任意的t∈R恒成立是解题的关键。
恒成立,转化为t2-2t+3>1-k任意的t∈R恒成立是解题的关键。

练习册系列答案
相关题目
 ,其中常数a > 0.
,其中常数a > 0. 上是减函数;
上是减函数; 上的函数
上的函数 ,对于任意的实数
,对于任意的实数 ,恒有
,恒有 ,且当
,且当 时,
时, 。
。 及
及 的值域。
的值域。 ,
, ,
, ,求
,求 的范围。
的范围。 为奇函数,
为奇函数,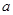 为常数,
为常数, 在区间
在区间 上单调递增;
上单调递增; 上的每一个
上的每一个 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.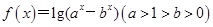 .
. 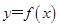 的定义域;
的定义域;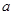 ,b满足什么条件时,
,b满足什么条件时,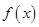 在
在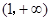 上恒取正值.
上恒取正值. 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里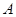 处,如图,现假设:①失事船的移动路径可视为抛物线
处,如图,现假设:①失事船的移动路径可视为抛物线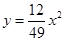 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发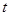 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为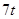

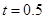 时,写出失事船所在位置
时,写出失事船所在位置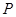 的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可) (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.  (a>0,a≠1).
(a>0,a≠1).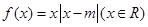 ,且
,且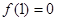 .
.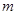 的值,并用分段函数的形式来表示
的值,并用分段函数的形式来表示 ;
;