题目内容
【题目】已知函数f(x)=ax2-2x+1.
(1)试讨论函数f(x)的单调性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
(3)在(2)的条件下,求证:g(a)≥![]() .
.
【答案】(1)见解析.(2)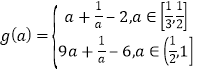 ;(3)详见解析.
;(3)详见解析.
【解析】
(1)分成![]() 三类,讨论函数的单调区间.(2)对函数进行配方,根据对称轴的位置对参数
三类,讨论函数的单调区间.(2)对函数进行配方,根据对称轴的位置对参数![]() 进行分类讨论,由此求得最大值和最小值,也即
进行分类讨论,由此求得最大值和最小值,也即![]() 的表达式.(3)利用导数求得
的表达式.(3)利用导数求得![]() 的单调区间,由此求得
的单调区间,由此求得![]() 的最小值,以此证明不等式成立.
的最小值,以此证明不等式成立.
(1)当a=0时,函数f(x)=-2x+1在(-∞,+∞)上为减函数;
当a>0时,抛物线f(x)=ax2-2x+1开口向上,对称轴为x=![]() ,
,
故函数f(x)在![]() 上为减函数,在
上为减函数,在![]() 上为增函数;
上为增函数;
当a<0时,抛物线f(x)=ax2-2x+1开口向下,对称轴为x=![]() ,
,
故函数f(x)在![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
(2)∵f(x)=a![]() 2+1-
2+1-![]() ,
,
由![]() ≤a≤1得1≤
≤a≤1得1≤![]() ≤3,∴N(a)=f
≤3,∴N(a)=f![]() =1-
=1-![]() .
.
当1≤![]() <2,即
<2,即![]() <a≤1时,M(a)=f(3)=9a-5,
<a≤1时,M(a)=f(3)=9a-5,
故g(a)=9a+![]() -6;
-6;
当2≤![]() ≤3,即
≤3,即![]() ≤a≤
≤a≤![]() 时,M(a)=f(1)=a-1,
时,M(a)=f(1)=a-1,
故g(a)=a+![]() -2.
-2.
∴g(a)=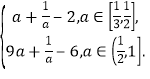
(3)证明:当a∈![]() 时,g′(a)=1-
时,g′(a)=1-![]() <0,
<0,
∴函数g(a)在![]() 上为减函数;
上为减函数;
当a∈![]() 时,g′(a)=9-
时,g′(a)=9-![]() >0,
>0,
∴函数g(a)在![]() 上为增函数,
上为增函数,
∴当a=![]() 时,g(a)取最小值,g(a)min=
时,g(a)取最小值,g(a)min=![]() =
=![]() .
.
故g(a)≥![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某地区为了解群众上下班共享单车使用情况,根据年龄按分层抽样的方式调查了该地区50名群众,他们的年龄频数及使用共享单车人数分布如下表:
年龄段 | 20~29 | 30~39 | 40~49 | 50~60 |
频数 | 12 | 18 | 15 | 5 |
经常使用共享单车 | 6 | 12 | 5 | 1 |
(1)由以上统计数据完成下面的![]() 列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | |||
不经常使用共享单车 | |||
总计 |
附: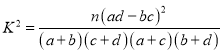 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(2)若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人,再从这6人中随机抽取2人,求这2人中恰好有1人年龄在30~39岁的概率.

