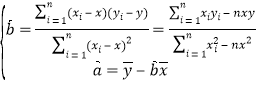题目内容
【题目】已知![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() (其中
(其中![]() ,且t为常数)时,
,且t为常数)时,![]() 是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由;
是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由;
(2)当![]() 时,求满足不等式
时,求满足不等式![]() 的实数x的取值范围.
的实数x的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)先判定函数的单调性,结合单调性来进行求解![]() 是否存在最小值;
是否存在最小值;
(2)先判断函数的奇偶性及单调性,结合奇偶性和单调性把![]() 进行转化求解.
进行转化求解.
(1)由![]() 可得
可得![]() 或
或![]() ,解得
,解得![]() ,即函数
,即函数![]() 的定义域为
的定义域为![]() ,
,
设![]() ,则
,则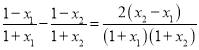 ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
①当![]() 时
时![]() ,则
,则![]() 在
在![]() 上是减函数,又
上是减函数,又![]() ,
,
∴![]() 时,
时,![]() 有最小值,且最小值为
有最小值,且最小值为![]() ;
;
②当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,
,
∴![]() 时,
时,![]() 无最小值.
无最小值.
(2)由于![]() 的定义域为
的定义域为![]() ,定义域关于原点对称,且
,定义域关于原点对称,且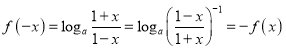 ,所以函数
,所以函数![]() 为奇函数.由(1)可知,当
为奇函数.由(1)可知,当![]() 时,函数
时,函数![]() 为减函数,由此,不等式
为减函数,由此,不等式![]() 等价于
等价于![]() ,即有
,即有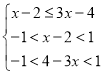 ,解得
,解得![]() ,所以x的取值范围是
,所以x的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: