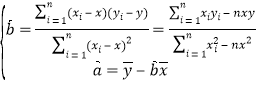题目内容
【题目】如图,已知扇形的圆心角∠AOB=![]() ,半径为
,半径为![]() ,若点C是
,若点C是![]() 上的一动点(不与点A,B重合).
上的一动点(不与点A,B重合).

(1)若弦![]() ,求
,求![]() 的长;
的长;
(2)求四边形OACB面积的最大值.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(1)在三角形![]() 中,利用余弦定理求得
中,利用余弦定理求得![]() 的余弦值,进而求得
的余弦值,进而求得![]() 的大小,再利用弧长公式计算出
的大小,再利用弧长公式计算出![]() 的长.
的长.
(2)设![]() ,利用三角形
,利用三角形![]() 和三角形
和三角形![]() 的面积表示出四边形
的面积表示出四边形![]() 的面积,利用三角恒等变换进行化简,结合三角函数最值的求法,求得四边形
的面积,利用三角恒等变换进行化简,结合三角函数最值的求法,求得四边形![]() 的面积的最大值.
的面积的最大值.
(1)在△OBC中,BC=4(![]() -1),OB=OC=
-1),OB=OC=![]() ,
,
所以由余弦定理得cos∠BOC=![]() ,
,
所以∠BOC=![]() ,
,
于是![]() 的长为
的长为![]() ×
×![]() =
=![]() .
.
(2)设∠AOC=θ,θ∈![]() ,则∠BOC=
,则∠BOC=![]() -θ,
-θ,
S四边形OACB=S△AOC+S△BOC=![]() ×
×![]() ×
×![]() sin θ
sin θ![]() ×
×![]() ×
×![]() ·sin
·sin![]() =24sin θ+
=24sin θ+![]() cos θ=
cos θ=![]() ,由于θ∈
,由于θ∈![]() ,所以
,所以![]() ,当θ=
,当θ=![]() 时,四边形OACB的面积取得最大值16
时,四边形OACB的面积取得最大值16![]() .
.

练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: