题目内容
3．已知（4，2）是直线l被椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1所截得的线段的中点，则l的方程是（ ）| A． | x+2y+8=0 | B． | x+2y-8=0 | C． | x-2y-8=0 | D． | x-2y+8=0 |
分析 设直线l与椭圆交于P1（x1，y1）、P2（x2，y2），由“点差法”可求出直线l的斜率．再由由点斜式可得l的方程．
解答 解：设直线l与椭圆交于P1（x1，y1）、P2（x2，y2），
（4，2）是直线l被椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1所截得的线段的中点，
将P1、P2两点坐标代入椭圆方程$\frac{{{x}_{1}}^{2}}{36}$+$\frac{{{y}_{1}}^{2}}{9}$=1，$\frac{{{x}_{2}}^{2}}{36}$+$\frac{{{y}_{2}}^{2}}{9}$=1相减得直线l斜率：
k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{4（{y}_{1}+{y}_{2}）}$=-$\frac{\frac{{x}_{1}+{x}_{2}}{2}}{\frac{4（{y}_{1}+{y}_{2}）}{2}}$=-$\frac{4}{4×2}$=-$\frac{1}{2}$．
由点斜式可得l的方程为x+2y-8=0．
故选：B．
点评 本题考查椭圆的中点弦方程，解题的常规方法是“点差法”．又叫平方差法．
练习册系列答案
相关题目
14．已知函数y-1=logax，则该函数恒过定点（ ）
| A． | （0，1） | B． | （1，1） | C． | （1，-1） | D． | （1，0） |
18．已知定义在R上奇函数f（x）满足f（1+x）=f（1-x）且f（x）在区间[3，5]上单调递增，则函数f（x）在区间[1，3]上的（ ）
| A． | 最大值是f（1），最小值是f（3） | B． | 最大值是f（3），最小值是f（1） | ||
| C． | 最大值是f（1），最小值是f（2） | D． | 最大值是f（2），最小值是f（3） |
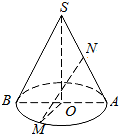已知圆锥的底面半径r=2，半径OM与母线SA垂直，N是SA中点，NM与高SO所成的角为α，tanα=2．则圆锥的体积为$\frac{4\sqrt{5}}{3}π$．