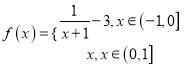Question

【题目】在某校组织的“共筑中国梦”竞赛活动中，甲、乙两班各有6名选手参赛，在第一轮笔试环节中，评委将他们的笔试成绩作为样本数据，绘制成如图所示的茎叶图，为了增加结果的神秘感，主持人故意没有给出甲、乙两班最后一位选手的成绩，知识告知大家，如果某位选手的成绩高于90分（不含90分），则直接“晋级”．

（1）求乙班总分超过甲班的概率；

（2）主持人最后宣布：甲班第六位选手的得分是90分，乙班第六位选手的得分是97分，

①请你从平均分和方差的角度来分析两个班的选手的情况；

②主持人从甲乙两班所有选手成绩中分别随机抽取2个，记抽取到“晋级”选手的总人数为，求的分布列及数学期望．

Answer 1

【答案】（1）；（2）见解析.

【解析】试题分析：（1）先分别求出甲班前 位选手的总分和乙班前 位选手的总分，由此利用列举法能求出乙班总分超过甲班的概率．

（2）①分别求出甲、乙两班平均分和方差，由此能求出甲班选手间的实力相当，相差不大，乙班选手间实力悬殊，差距较大．

②ξ的可能取值为，，，，，分别求出相应的概率，由此能求出的分布列和．

试题解析：

（1）甲班前5位选手的总分为，

乙班前5位选手的总分为，

若乙班总分超过甲班，则甲、乙两班第六位选手的成绩可分别为，，三种．

所以，乙班总分超过甲班的概率为．

（2）①甲班平均分为，

乙班平均分为，

，．

两班的平均分相同，但甲班选手的方差小于乙班，所以甲班选手间的实力相当，相差不大，乙班选手间实力悬殊，差距较大．

②的可能取值为，，，，，

；；；；．

∴的分布列为：

	0	1	2	3	4

∴ .