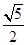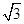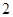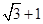题目内容
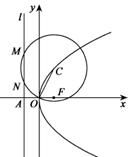
如图,抛物线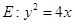 的焦点为F,准线
的焦点为F,准线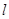 与x轴的交点为A.点C在抛物线E上,以C为圆心,
与x轴的交点为A.点C在抛物线E上,以C为圆心,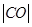 为半径作圆,设圆C与准线
为半径作圆,设圆C与准线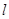 交于不同的两点M,N.
交于不同的两点M,N.
(I)若点C的纵坐标为2,求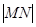 ;
;
(II)若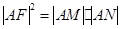 ,求圆C的半径.
,求圆C的半径.
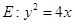 的焦点为F,准线
的焦点为F,准线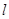 与x轴的交点为A.点C在抛物线E上,以C为圆心,
与x轴的交点为A.点C在抛物线E上,以C为圆心,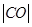 为半径作圆,设圆C与准线
为半径作圆,设圆C与准线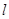 交于不同的两点M,N.
交于不同的两点M,N.
(I)若点C的纵坐标为2,求
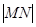 ;
;(II)若
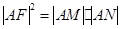 ,求圆C的半径.
,求圆C的半径.(I)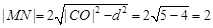 (II)
(II)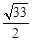
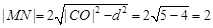 (II)
(II)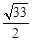
(Ⅰ)抛物线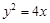 的准线
的准线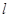 的方程为
的方程为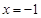 ,
,
由点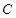 的纵坐标为
的纵坐标为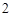 ,得点
,得点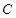 的坐标为
的坐标为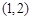
所以点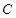 到准线
到准线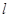 的距离
的距离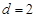 ,又
,又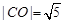 .
.
所以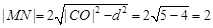 .
.
(Ⅱ)设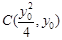 ,则圆
,则圆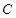 的方程为
的方程为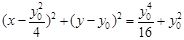 ,
,
即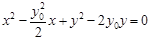 .
.
由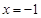 ,得
,得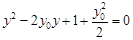
设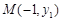 ,
,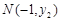 ,则:
,则:
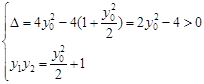
由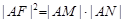 ,得
,得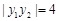
所以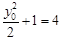 ,解得
,解得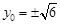 ,此时
,此时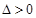
所以圆心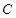 的坐标为
的坐标为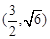 或
或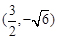
从而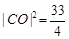 ,
,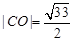 ,即圆
,即圆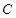 的半径为
的半径为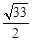
此题以圆为背景考查了解析几何中的常用方法(如设而不求)及圆锥曲线的性质.平时只要注意计算此题问题就不会太大.
【考点定位】 本题考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识,考查运算求解 能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想.属于中等难度.
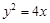 的准线
的准线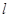 的方程为
的方程为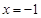 ,
,由点
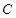 的纵坐标为
的纵坐标为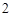 ,得点
,得点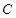 的坐标为
的坐标为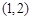
所以点
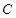 到准线
到准线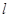 的距离
的距离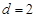 ,又
,又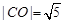 .
.所以
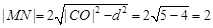 .
.(Ⅱ)设
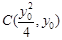 ,则圆
,则圆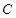 的方程为
的方程为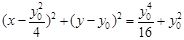 ,
,即
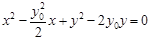 .
.由
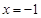 ,得
,得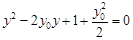
设
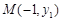 ,
,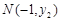 ,则:
,则: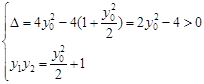
由
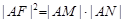 ,得
,得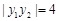
所以
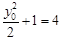 ,解得
,解得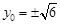 ,此时
,此时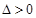
所以圆心
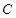 的坐标为
的坐标为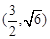 或
或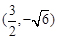
从而
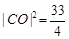 ,
,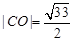 ,即圆
,即圆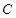 的半径为
的半径为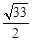
此题以圆为背景考查了解析几何中的常用方法(如设而不求)及圆锥曲线的性质.平时只要注意计算此题问题就不会太大.
【考点定位】 本题考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识,考查运算求解 能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想.属于中等难度.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
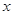 轴上,一个顶点为
轴上,一个顶点为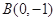 ,且其右焦点到直线
,且其右焦点到直线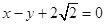 的距离为3.
的距离为3.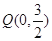 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点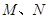 ,且满足
,且满足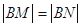 .
.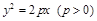 的焦点为
的焦点为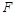 ,
,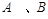 在抛物线上,且
在抛物线上,且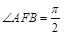 ,弦
,弦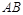 的中点
的中点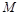 在其准线上的射影为
在其准线上的射影为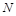 ,则
,则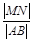 的最大值为________。
的最大值为________。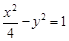 的顶点到渐进线的距离等于( )
的顶点到渐进线的距离等于( )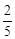

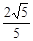
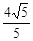
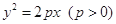 的焦点为
的焦点为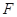 ,
,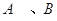 在抛物线上,且
在抛物线上,且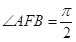 ,弦
,弦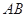 的中点
的中点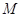 在其准线上的射影为
在其准线上的射影为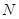 ,则
,则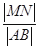 的最大值为
的最大值为
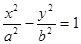 与
与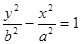 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为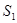 ,连接其四个焦点组成的四边形的面积为
,连接其四个焦点组成的四边形的面积为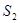 ,则
,则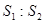 的最大值是
的最大值是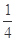
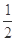
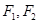 是椭圆
是椭圆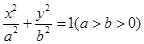 的左、右焦点,
的左、右焦点,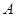 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点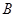 也在椭圆上,且满足
也在椭圆上,且满足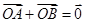 (
(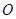 是坐标原点),
是坐标原点),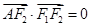 ,若椭圆的离心率为
,若椭圆的离心率为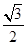 .
.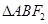 的面积等于
的面积等于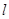 与(1)中的椭圆相交于不同的两点
与(1)中的椭圆相交于不同的两点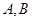 ,已知点
,已知点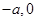 ),点
),点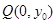 在线段
在线段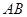 的垂直平分线上,且
的垂直平分线上,且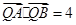 ,求
,求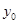 的值.
的值. 的双曲线的焦点在x轴上,且过点P
的双曲线的焦点在x轴上,且过点P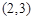 .
.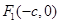 ,
,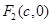 分别是双曲线
分别是双曲线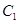 :
: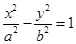
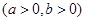 的两个焦点,双曲线
的两个焦点,双曲线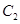 :
: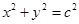 的一个交点为
的一个交点为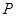 ,且
,且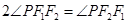 ,那么双曲线
,那么双曲线