题目内容
已知焦距为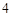 的双曲线的焦点在x轴上,且过点P
的双曲线的焦点在x轴上,且过点P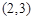 .
.
(Ⅰ)求该双曲线方程 ;
(Ⅱ)若直线m经过该双曲线的右焦点且斜率为1,求直线m被双曲线截得的弦长.
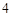 的双曲线的焦点在x轴上,且过点P
的双曲线的焦点在x轴上,且过点P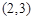 .
.(Ⅰ)求该双曲线方程 ;
(Ⅱ)若直线m经过该双曲线的右焦点且斜率为1,求直线m被双曲线截得的弦长.
(1) 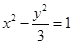 ;(2)|AB|="6" 。
;(2)|AB|="6" 。
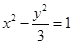 ;(2)|AB|="6" 。
;(2)|AB|="6" 。试题分析:(1)设双曲线方程为(a,b>0)
左右焦点F1、F2的坐标分别为(-2,0)(2,0) 1分
则|PF1|-|PF2|=2=2
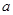 ,所以
,所以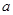 =1, ,3分
=1, ,3分又c=2,b=
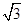 5分
5分所以方程为
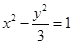 6分
6分(2)直线m方程为y=x-2 7分
联立双曲线及直线方程消y得2 x2 +4x-7=0 9分
设两交点
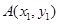 ,
,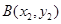 x1+x2=-2, x1x2=-3.5 10分
x1+x2=-2, x1x2=-3.5 10分由弦长公式得|AB|=6 12分
点评:中档题,求圆锥曲线的标准方程,往往利用定义或曲线的几何性质,确定a,b,c,e等。涉及直线与圆锥曲线的位置关系问题,往往联立方程组,应用韦达定理,简化解题过程。本题直接利用弦长公式,计算较为简便。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
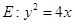 的焦点为F,准线
的焦点为F,准线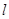 与x轴的交点为A.点C在抛物线E上,以C为圆心,
与x轴的交点为A.点C在抛物线E上,以C为圆心,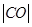 为半径作圆,设圆C与准线
为半径作圆,设圆C与准线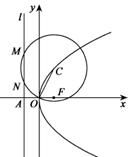
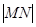 ;
;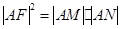 ,求圆C的半径.
,求圆C的半径.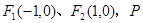 是椭圆上一点且
是椭圆上一点且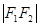 是
是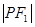 与
与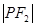 的等差中项,则此椭圆的标准方程为 。
的等差中项,则此椭圆的标准方程为 。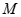 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0,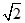 ),(0,
),(0,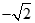 ),又点
),又点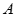
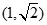 在椭圆
在椭圆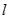 的斜率为
的斜率为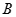 、
、 两点,求
两点,求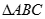 面积的最大值.
面积的最大值.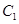 的焦点与椭圆
的焦点与椭圆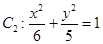 的右焦点重合,抛物线
的右焦点重合,抛物线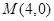 的直线
的直线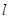 与抛物线
与抛物线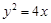 的焦点为
的焦点为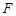 ,点
,点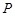 为抛物线上的动点,点
为抛物线上的动点,点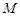 为其准线上的动点,当
为其准线上的动点,当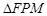 为等边三角形时,其面积为
为等边三角形时,其面积为 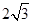
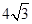
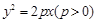 的焦点为
的焦点为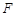 ,点
,点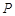 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,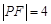 .
.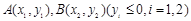 是抛物线上的两点,
是抛物线上的两点,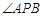 的角平分线与
的角平分线与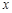 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;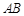 过点
过点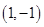 ,求弦
,求弦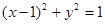 的切线(P点不在y轴上).
的切线(P点不在y轴上).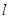 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使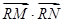 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。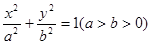 与
与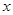 轴负半轴交于点
轴负半轴交于点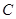 ,
,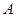 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线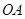 交椭圆于另一点
交椭圆于另一点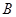 ,椭圆左焦点为
,椭圆左焦点为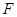 ,连接
,连接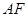 交
交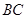 于点D。
于点D。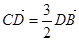 ,求椭圆的离心率;
,求椭圆的离心率; 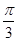 且△ABC的面积为
且△ABC的面积为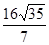 ,求椭圆的标准方程。
,求椭圆的标准方程。