题目内容
1.命题p:直线y=kx+2与圆x2+y2=1相交于A,B两点;命题q:曲线$\frac{{x}^{2}}{16-k}$-$\frac{{y}^{2}}{k}$=1表示焦点在x轴上的双曲线,若p∧q为真命题,求实数k的取值范围.分析 先求出命题p,q为真时k的范围,再由p∧q为真命题,得到p,q均为真命题,得到不等式组,从而求出k的范围.
解答 解:∵命题p:直线y=kx+2与圆x2+y2=1相交于A,B两点,
∴圆心到直线的距离d=$\frac{|k•0-0+2|}{\sqrt{{k}^{2}+1}}$<1,
∴k$>\sqrt{3}$或k<-$\sqrt{3}$,
∵命题q:曲线$\frac{{x}^{2}}{16-k}$-$\frac{{y}^{2}}{k}$=1表示焦点在x轴上的双曲线,
∴$\left\{\begin{array}{l}{16-k>0}\\{k>0}\end{array}\right.$,
解得0<k<16,
∵p∧q为真命题,
∴p,q均为真命题,
∴$\left\{\begin{array}{l}{0<k<16}\\{k>\sqrt{3}或k<-\sqrt{3}}\end{array}\right.$,
∴$\sqrt{3}$<k<16.
点评 本题以复合命题的真假为载体,考查双曲线的标准方程及性质,以及直线和圆的位置关系,准确记住这些概念性质是解题的关键,本题是一道基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积是( )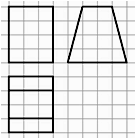

| A. | 42+6$\sqrt{17}$ | B. | 30+6$\sqrt{17}$ | C. | 66 | D. | 44 |
12.若a和b是计算机在区间(0,2)上产生的随机数,那么函数f(x)=lg(ax2+4x+4b)的定义域为R(实数集)的概率为( )
| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
6.复数(1-4i)2的虚部为( )
| A. | -4i | B. | -4 | C. | -8i | D. | -8 |
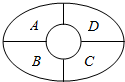 如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.
如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.