Question

【题目】已知椭圆 的左、右焦点分别为F1 ， F2 ， 上顶点为B，若△BF1F2的周长为6，且点F1到直线BF2的距离为b． （Ⅰ）求椭圆C的方程；
（Ⅱ）设A1 ， A2是椭圆C长轴的两个端点，点P是椭圆C上不同于A1 ， A2的任意一点，直线A1P交直线x=m于点M，若以MP为直径的圆过点A2 ， 求实数m的值．

Answer 1

【答案】解：（Ⅰ）由已知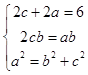得 ，解得 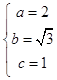． 所以椭圆C的方程为 ．
（Ⅱ）由题意知A1（﹣2，0），A2（2，0），
设P（x0 ， y0），则 ，得 ．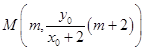
且由点P在椭圆上，得 ．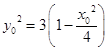
若以MP为直径的圆过点A2 ， 则 ，
所以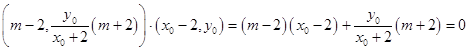
因为点P是椭圆C上不同于A1 ， A2的点，所以x0≠±2．
所以上式可化为 ，解得m=14．
【解析】（Ⅰ）由已知列出方程，求出a，b，即可得到椭圆方程．（Ⅱ）由题意知A1（﹣2，0），A2（2，0），设P（x0 ， y0），求出M坐标，由点P在椭圆上，以MP为直径的圆过点A2 ， 则 ，求出x0≠±2．然后求解m即可．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．