题目内容
【题目】已知f(x)=(x2﹣3)ex(其中x∈R,e是自然对数的底数),当t1>0时,关于x的方程[f(x)﹣t1][f(x)﹣t2]=0恰好有5个实数根,则实数t2的取值范围是( )
A.(﹣2e,0)
B.(﹣2e,0]
C.[﹣2e,6e﹣3]
D.(﹣2e,6e﹣3)
【答案】D
【解析】解:f(x)=(x2﹣3)ex的导数为 f′(x)=(x2+2x﹣3)ex=(x﹣1)(x+3)ex ,
当﹣3<x<1时,f′(x)<0,f(x)递减;
当x>1或x<﹣3时,f′(x)>0,f(x)递增.
可得f(x)的极小值为f(1)=﹣2e,极大值为f(﹣3)=6e﹣3 ,
作出y=f(x)的图象,如图:
当t1>0时,关于x的方程[f(x)﹣t1][f(x)﹣t2]=0
恰好有5个实数根,
即为f(x)=t1或f(x)=t2恰好有5个实数根,
若t1>6e﹣3 , f(x)=t1只有一个实根,不合题意;
若0<t1<6e﹣3 , f(x)=t1有三个实根,只要﹣2e<t2≤0,满足题意;
若t1=6e﹣3 , f(x)=t1有两个实根,只要0<t2<6e﹣3 , 满足题意;
综上可得,t2的范围是(﹣2e,6e﹣3).
故选:D.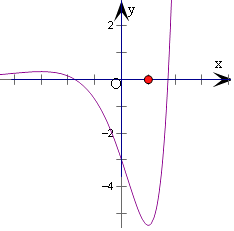

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目