题目内容
【题目】已知等差数列
中，
．
（1）求数列的通项；
（2）满足
的共有几项？
【答案】（1）
（2）23项．
【解析】
（1）设首项为
，公差为d，根据题中条件，建立关于
的方程组，求解得到
，进而得到其通项公式；
（2）结合（1）中所求的等差数列的通项公式，建立关于
的不等式组，结合
的条件，求得结果.
（1）解法一 设首项为，公差为d，由已知，得
解方程组，得
．
解法二 利用等差数列的性质，得
，即
．
解方程，得
．
．
解法三 因为等差数列
是关于n的一次函数，所以
三点共线，即
．整理，得．
（2）由
，又，
．解不等式，得
，取整数共有23项．
说明 本例中第（1）问的解法一利用等差数列基本量和d的运算；解法二利用等差数列的基本性质；解法三体现了函数思想方法在数列中的运用．
练习册系列答案
相关题目
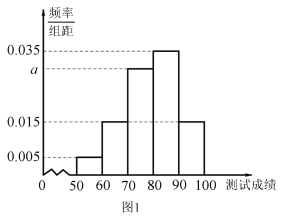
【题目】顺义区教委对本区高一，高二年级学生体质健康测试成绩进行抽样分析.学生测试成绩满分为100分，90分及以上为优秀，60分以下为不及格.先从两个年级各抽取100名学生的测试成绩.其中高一年级学生测试成绩统计结果如图1，高二年级学生测试成绩统计结果如表1.
分组 | 人数 |
|
|
|
|
|
|
|
|
|
|
表1
（1）求图1中a的值；
（2）为了调查测试成绩不及格的同学的具体情况，决定从样本中不及格的学生中抽取3人，用X表示抽取的3人中高二年级的学生人数.求X的分布列及均值；
（3）若用以上抽样数据估计全区学生体质健康情况.用Y表示从全区高二年级全部学生中任取3人中成绩优秀的人数，求EY的值；
（4）用
，
，分别表示样本中高一，高二年级学生测试成绩的方差，比较其大小（只需写出结果）.
