题目内容
10.设函数f(x)=lnx+a(x2-1)-2(x-1).(Ⅰ)若a=0时直线y=mx+1与曲线y=f(x)相切,求m的值;
(Ⅱ)已知(x-1)f(x)≥0,求a的取值范围.
分析 (Ⅰ)求得a=0的f(x)的解析式,求得导数,设出切点,求得切线的斜率,结合切线方程,计算即可得到m=-1;
(Ⅱ)讨论x≥1时,f(x)≥0,或x≤1,f(x)≤0,考虑等价变形$\frac{lnx}{x-1}$≥2-a(x+1),即有y=$\frac{lnx}{x-1}$恒在直线y=2-a(x+1)上,画出图象,结合直线恒过定点(-1,2),观察即可得到a的范围.
解答 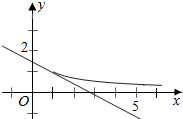 解:(Ⅰ)若a=0时,f(x)=lnx-2(x-1),
解:(Ⅰ)若a=0时,f(x)=lnx-2(x-1),
f′(x)=$\frac{1}{x}$-2,设切点为(s,t),
则$\frac{1}{s}$-2=m,ms+1=lns-2(s-1),
解得s=1,m=-1.
(Ⅱ)由(x-1)f(x)≥0,可得
x≥1时,f(x)≥0,或x≤1,f(x)≤0,
当x≥1时,lnx+a(x2-1)-2(x-1)≥0,
即为$\frac{lnx}{x-1}$+a(x+1)-2≥0,
即有$\frac{lnx}{x-1}$≥2-a(x+1),
即有y=$\frac{lnx}{x-1}$恒在直线y=2-a(x+1)上,
由于$\frac{lnx}{x-1}$-1=$\frac{lnx-x+1}{x-1}$,由lnx-x+1的导数为$\frac{1}{x}$-1<0,
可得lnx<x-1,即有$\frac{lnx}{x-1}$<1,
则有0<$\frac{lnx}{x-1}$<1.
由图象可知直线过点(1,1)时,1=2-a(1+1),
可得a=$\frac{1}{2}$,
即有a≥$\frac{1}{2}$;
同理可得0<x≤1,f(x)≤0恒成立,
即为lnx+a(x2-1)-2(x-1)≤0,
即为$\frac{lnx}{x-1}$+a(x+1)-2≥0,
即有$\frac{lnx}{x-1}$≥2-a(x+1),
即有y=$\frac{lnx}{x-1}$恒在直线y=2-a(x+1)上,
即有a≥$\frac{1}{2}$.
综上可得a的范围是[$\frac{1}{2}$,+∞).
点评 本题考查导数的运用:求切线的斜率,考查不等式成立问题的解法,注意通过数形结合的思想方法,属于中档题.

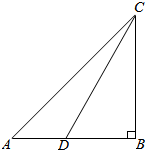 如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.
如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| 对iPhone6的态度 | 计划购买的女员工 | 不计划购买的女员工 | 计划购买的男员工 | 不计划购买的男员工 |
| 频数 | 200 | 600 | 400 | 800 |
(2)若从计划购买的员工中按照性别分层抽样的方法抽取6人进行座谈,再从这6人中随机选取2人分别赠送苹果公司最新产品各一台,记获得赠品的女员工人数为X,试求X的分布列及期望.