题目内容
3.直线l1的极坐标系方程为ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$,直线l2的参数方程为$\left\{\begin{array}{l}{x=1-2t}\\{y=4t+3}\end{array}\right.$(t为参数),则l1与l2的交点A的直角坐标是(3,-1).分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$可把直线l1的极坐标系方程ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$,化为直角坐标方程;直线l2的参数方程$\left\{\begin{array}{l}{x=1-2t}\\{y=4t+3}\end{array}\right.$(t为参数),消去参数t化为普通方程,联立解出即可.
解答 解:直线l1的极坐标系方程ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$,展开化为:$\frac{\sqrt{2}}{2}$(ρcosθ+ρsinθ)=$\sqrt{2}$,∴x+y=2.
直线l2的参数方程$\left\{\begin{array}{l}{x=1-2t}\\{y=4t+3}\end{array}\right.$(t为参数),消去参数t化为2x+y=5.
联立$\left\{\begin{array}{l}{x+y=2}\\{2x+y=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
∴l1与l2的交点A的直角坐标是(3,-1).
故答案为:(3,-1).
点评 本题考查了极坐标系方程化为直角坐标方程、直线的参数方程化为普通方程、直线的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.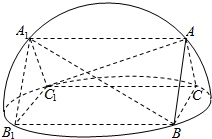 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上,且AB=AC,B1C1=$\sqrt{2}$BB1,则异面直线AC1与A1B所成的角为( )
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上,且AB=AC,B1C1=$\sqrt{2}$BB1,则异面直线AC1与A1B所成的角为( )
 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上,且AB=AC,B1C1=$\sqrt{2}$BB1,则异面直线AC1与A1B所成的角为( )
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上,且AB=AC,B1C1=$\sqrt{2}$BB1,则异面直线AC1与A1B所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
12.(ax+$\frac{1}{x}$)(2x-1)5的展开式中各项系数的和为2,则a的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
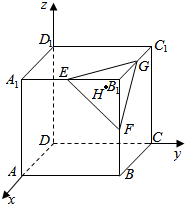 如图,在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1,E,F,G,分别为A1B1,B1C1,BB1的中点,H为△EFG的重心,求DH的长度.
如图,在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1,E,F,G,分别为A1B1,B1C1,BB1的中点,H为△EFG的重心,求DH的长度.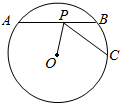 如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )
如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )