题目内容
17.已知双曲线的渐近线方程为x±2y=0,且双曲线过点M(4,$\sqrt{3}$),则双曲线的方程为x2-4y2=4.分析 依题意,可设所求的双曲线的方程为(x+2y)(x-2y)=λ,将点M(4,$\sqrt{3}$)的坐标代入求得λ即可.
解答 解:设所求的双曲线的方程为(x+2y)(x-2y)=λ,
∵点M(4,$\sqrt{3}$)为该双曲线上的点,
∴λ=(4+2$\sqrt{3}$)(4-2$\sqrt{3}$)=4,
∴该双曲线的方程为:x2-4y2=4.
故答案为:x2-4y2=4.
点评 本题考查双曲线的简单性质,着重考查待定系数法的应用,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.世界人口在过去40年内翻了一番,则每年人口平均增长率是(参考数据lg2≈0.3010,100.0075≈1.017)( )
| A. | 1.5% | B. | 1.6% | C. | 1.7% | D. | 1.8% |
4.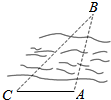 如图,设A,B两点在河的两岸,一测量者在A的同侧选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°,则A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在A的同侧选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°,则A,B两点的距离为( )
 如图,设A,B两点在河的两岸,一测量者在A的同侧选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°,则A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在A的同侧选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°,则A,B两点的距离为( )| A. | 50$\sqrt{2}$ m | B. | 50 m | C. | 25 m | D. | 25$\sqrt{2}$ m |