题目内容
10．曲线y=x3-4x2+4在点（1，1）处的切线方程为（ ）| A． | y=-x+2 | B． | y=5x-4 | C． | y=-5x+6 | D． | y=x-1 |
分析 求出函数y=x3-4x2+4在x=1处的导数值，这个导数值即函数图象在该点处的切线的斜率，然后根据直线的点斜式方程求解即可．
解答 解：由曲线y=x3-4x2+4，
所以y′=3x2-8x，
曲线y=x3-4x2+4点（1，1）处的切线的斜率为：y′|x=1=3-8=-5．
此处的切线方程为：y-1=-5（x-1），即y=-5x+6．
故选：C．
点评 本题考查导数的几何意义、关键是求出直线的斜率，正确利用直线的点斜式方程，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．设m，n∈R，若直线（m+1）x+（n+1）y-2=0与圆（x-1）2+（y-1）2=1相切，则m+n的取值范围是（ ）
| A． | [2-2$\sqrt{2}$，2+2$\sqrt{2}$] | B． | （-∞，2-2$\sqrt{2}$]∪[2+2$\sqrt{2}$，+∞） | C． | [1-$\sqrt{3}$，1+$\sqrt{3}$] | D． | （-∞，1-$\sqrt{3}$}∪[1+$\sqrt{3}$，+∞） |
1．直线3x+y-5=0的斜率及在y轴上的截距分别是（ ）
| A． | $3，-\frac{5}{3}$ | B． | 3，5 | C． | -3，-5 | D． | -3，5 |
5．在一组样本数据（x1，y1），（x2，y2），…（xn，yn）（n≥2，x1，x2，…，xn不全相等）的散点图中，若所有样本点（xi，yi）（i=1，2，…，n）都在直线y=2x+1上，则这组样本数据的样本相关系数为（ ）
| A． | -1 | B． | 0 | C． | 2 | D． | 1 |
15．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2．若双曲线C上存在一点P，使得△PF1F2为等腰三角形，且cos∠PF1F2=$\frac{1}{8}$，则双曲线的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |
2．用秦九韶算法计算当x=2时，f（x）=3x4+x3+2x2+x+4的值的过程中，v2的值为（ ）
| A． | 3 | B． | 7 | C． | 16 | D． | 33 |
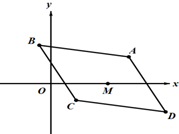如图，平行四边形ABCD（A，B，C，D按逆时针顺序排列），AB，AD边所在直线的方程分别是x+4y-7=0，3x+2y-11=0，且对角线AC和BD的交点为M（2，0）