题目内容
7.已知矩阵A=$[\begin{array}{l}{3}&{3}\\{2}&{4}\end{array}]$.(1)求矩阵A的逆矩阵A-1;
(2)求矩阵A的特征值和特征向量;
(3)求圆x2+y2=1在经过矩阵A对应的变换后得到的曲线的方程.
分析 (1)根据AA-1=$[\underset{\stackrel{1}{\;}}{0}$ $\underset{\stackrel{0}{\;}}{1}]$,求出A的逆矩阵A-1;
(2)根据矩阵A的特征多项式,求出A的特征值与特征向量;
(3)求出圆x2+y2=1上任意一点,经过矩阵A对应的变换后得到点满足的方程即可.
解答 解:(1)∵A=$[\underset{\stackrel{3}{\;}}{2}$ $\underset{\stackrel{3}{\;}}{4}]$,
AA-1=$[\underset{\stackrel{1}{\;}}{0}$ $\underset{\stackrel{0}{\;}}{1}]$,
∴A-1=$[\underset{\stackrel{\frac{2}{3}}{\;}}{-\frac{1}{3}}$ $\underset{\stackrel{-\frac{1}{2}}{\;}}{\frac{1}{2}}]$;
(2)矩阵A=$[\underset{\stackrel{3}{\;}}{2}$ $\underset{\stackrel{3}{\;}}{4}]$的特征多项式为:f(λ)=$|\underset{\stackrel{λ-3}{\;}}{-2}$ $\underset{\stackrel{-3}{\;}}{λ-4}|$=λ2-7λ+6;
令f(λ)=0,解得矩阵A的特征值为:λ1=6,λ2=1;
把λ1=6代入方程组$\left\{\begin{array}{l}{(λ-3)x-3y=0}\\{-2x+(λ-4)y=0}\end{array}\right.$,解得x=y,
所以矩阵A的属于特征值6的一个特征向量为α1=$[\underset{\stackrel{1}{\;}}{1}]$;
再把λ2=1代入方程组$\left\{\begin{array}{l}{(λ-3)x-3y=0}\\{-2x+(λ-4)=0}\end{array}\right.$,解得2x=-3y,
所以矩阵A的属于特征值1的一个特征向量为α2=$[\underset{\stackrel{3}{\;}}{-2}]$;
(3)设(x0,y0)是圆x2+y2=1上任意一点,
它在经过矩阵A对应的变换后得到点(x,y),
由$[\underset{\stackrel{x}{\;}}{y}]$=$[\underset{\stackrel{3}{\;}}{2}$ $\underset{\stackrel{3}{\;}}{4}]$ $[\underset{\stackrel{{x}_{0}}{\;}}{{y}_{0}}]$=$[\underset{\stackrel{{3x}_{0}+{3y}_{0}}{\;}}{{2x}_{0}+{4y}_{0}}]$,
得$\left\{\begin{array}{l}{x={3x}_{0}+{3y}_{0}}\\{y={2x}_{0}+{4y}_{0}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{0}=\frac{4x-3y}{6}}\\{{y}_{0}=\frac{-2x+3y}{6}}\end{array}\right.$;
代入${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=1,
整理得10x2+9y2-18xy-18=0,即为所求.
点评 本题考查了高等数学中的矩阵以及矩阵的变换应用问题,也考查了求矩阵的逆矩阵与特征向量的应用问题.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | 7 | B. | 2 | C. | 5 | D. | -7 |
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
| A. | 3 | B. | 7 | C. | 16 | D. | 33 |
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{x^2}{3}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{6}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{16}=1$ |
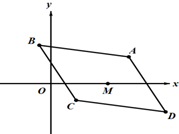 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)