题目内容
11.设数列{an}的前n项和Sn满足:Sn=n2,等比数列{bn}满足:b2=2,b5=16(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn.
分析 (1)由数列的通项和前n项和的关系,可得an的通项,由等比数列的通项可得;
(2)由错位相减法,可得数列{anbn}的前n项和Tn.
解答 解:(1){an}的前n项和Sn满足:Sn=n2,
n=1时,a1=S1=1,n>1时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
n=1也成立.
故an=2n-1,
等比数列{bn}满足:b2=2,b5=16,
q3=$\frac{{b}_{5}}{{b}_{2}}$=8,解得q=2.
则有bn=b2qn-2=2n-1;
(2)前n项和Tn=1•1+3•2+5•4+7•8+…+(2n-1)•2n-1,
2Tn=1•2+3•4+5•8+7•16+…+(2n-1)•2n,
两式相减.得-Tn=1+2•2+2•4+2•8+2•16+…+2•2n-1-(2n-1)•2n,
即有-Tn=1+$\frac{4(1-{2}^{n-1})}{1-2}$-(2n-1)•2n,
则有${T_n}=(2n-3){2^n}+3$.
点评 本题考查数列的通项和前n项和的关系,同时考查等比数列的通项和求和公式,及数列的求和:错位相减法,考查运算能力,属于中档题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
1.直线3x+y-5=0的斜率及在y轴上的截距分别是( )
| A. | $3,-\frac{5}{3}$ | B. | 3,5 | C. | -3,-5 | D. | -3,5 |
2.用秦九韶算法计算当x=2时,f(x)=3x4+x3+2x2+x+4的值的过程中,v2的值为( )
| A. | 3 | B. | 7 | C. | 16 | D. | 33 |
6.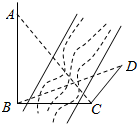 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
3.($\sqrt{x}$+$\frac{1}{\root{3}{x}}$)2n(n∈N*)展开式中只有第6项系数最大,则其常数项为( )
| A. | 120 | B. | 210 | C. | 252 | D. | 45 |
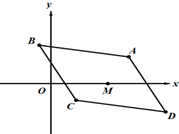 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)