题目内容
14.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下: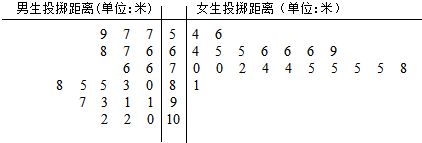
已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
分析 (Ⅰ)先把女生的数据从小到大排序,根据中位数和众数的定义即可求出;
(Ⅱ)掷距离低于7.0米的男生的得分如下:4,4,4,6,6,6.这6名男生分别记为A1,A2,A3,B1,B2,B3.列举出从这6名男生中随机抽取2名男生的所有可能的结果,在找到抽取的2名男生得分都是4分的基本事件,根据概率公式计算即可,
(Ⅲ)从平均数、方差、极差、中位数、众数等角度对整个年级学生掷实心球项目的情况进行合理的说明即可;也可以对整个年级男、女生该项目情况进行对比;或根据目前情况对学生今后在该项目的训练提出合理建议.
解答 解.(Ⅰ) 20名女生掷实心球得分如下:5,6,7,7,7,7,7,7,8,8,8,9,9,9,9,9,9,9,10,10.所以中位数为8,众数为9.
(Ⅱ) 由题意可知,掷距离低于7.0米的男生的得分如下:4,4,4,6,6,6.这6名男生分别记为A1,A2,A3,B1,B2,B3.从这6名男生中随机抽取2名男生,所有可能的结果有15种,它们是:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,B3),(A2,A3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),(B1,B2),(B1,B3),(B2,B3).
用C表示“抽取的2名男生得分均为(4分)”这一事件,则C中的结果有3个,它们是:(A1,A2),(A1,A3),(A2,A3).
所以,所求得概率$P(C)=\frac{3}{15}=\frac{1}{5}$.
(Ⅲ).例如:①估计该学校女生的得分的中位数和众数中位数为8,众数为9,
②成绩还需要提高,等等(合理即可).
点评 本题考查了中位数和众数的定义以及古典概型的概率问题,关键是用列举法表示所有的基本事件,属于基础题.

| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
| A. | 3 | B. | 7 | C. | 16 | D. | 33 |
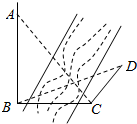 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
| A. | 120 | B. | 210 | C. | 252 | D. | 45 |
| A. | $\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{11}$ |
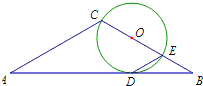 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.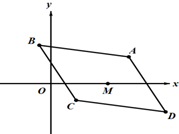 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)